柯尼斯堡七桥问题和汉密尔顿路径问题

这本计算的本质部头不小，英文版的，准备好好读一下，每次读一个小结，第一天看完之后给🐰讲的时候才发现这真的是一种好的看书方法，虽然费曼学习法的提出是不是费曼成疑，但这不失为一种好的方法。

1.1部分讲的是柯尼斯堡七桥问题

缘起于解决一个问题。柯尼斯堡有七座桥，有没有办法走遍每一座桥一次。对于这个问题，最直接的办法是进行穷举，但是穷举七座桥的情况比较简单，但对于威尼斯来说，穷举就很难了。

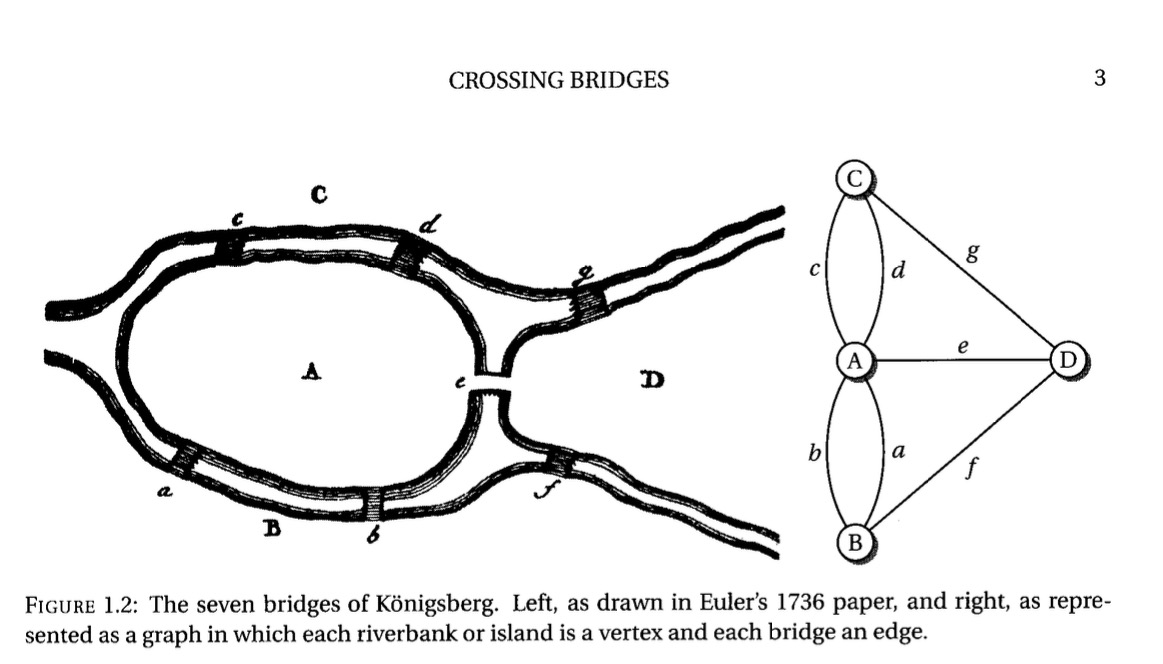
欧拉的解决办法是，图的每个顶点有几个边相连，就是几个度（degree）。结论就是一个图有欧拉环当且仅当一个图的每个顶点的度都是偶数，如果有两个是奇数，就是欧拉路径。

欧拉的方法很棒，原因在于，当你穷举给市民看所有的结果是，他也是冗长乏味的，不会有几个人耐心看完，或者直接质疑肯定有一个路径。这样的证明无疑是优雅，简洁的。欧拉转化了一个是否存在的问题的逻辑结构。

汉密尔顿问题是1.2中的问题。寻找汉密尔顿路径（Hamiltonian Path，即在图中访问每个顶点一次且仅一次的路径）是理论计算机科学中的一个核心问题。它最早来源于19世纪威廉·罗恩·哈密尔顿（William Rowan Hamilton）设计的”Icosian游戏”。这个游戏的目标是在正十二面体上行走，每个顶点只能访问一次。（这里没有提到边，但是一般来说不会这样，因为会导致不符合要求）。同样的还是有汉密尔顿路径和汉密尔顿环的概念，有汉密尔顿循环的图叫做汉密尔顿图。

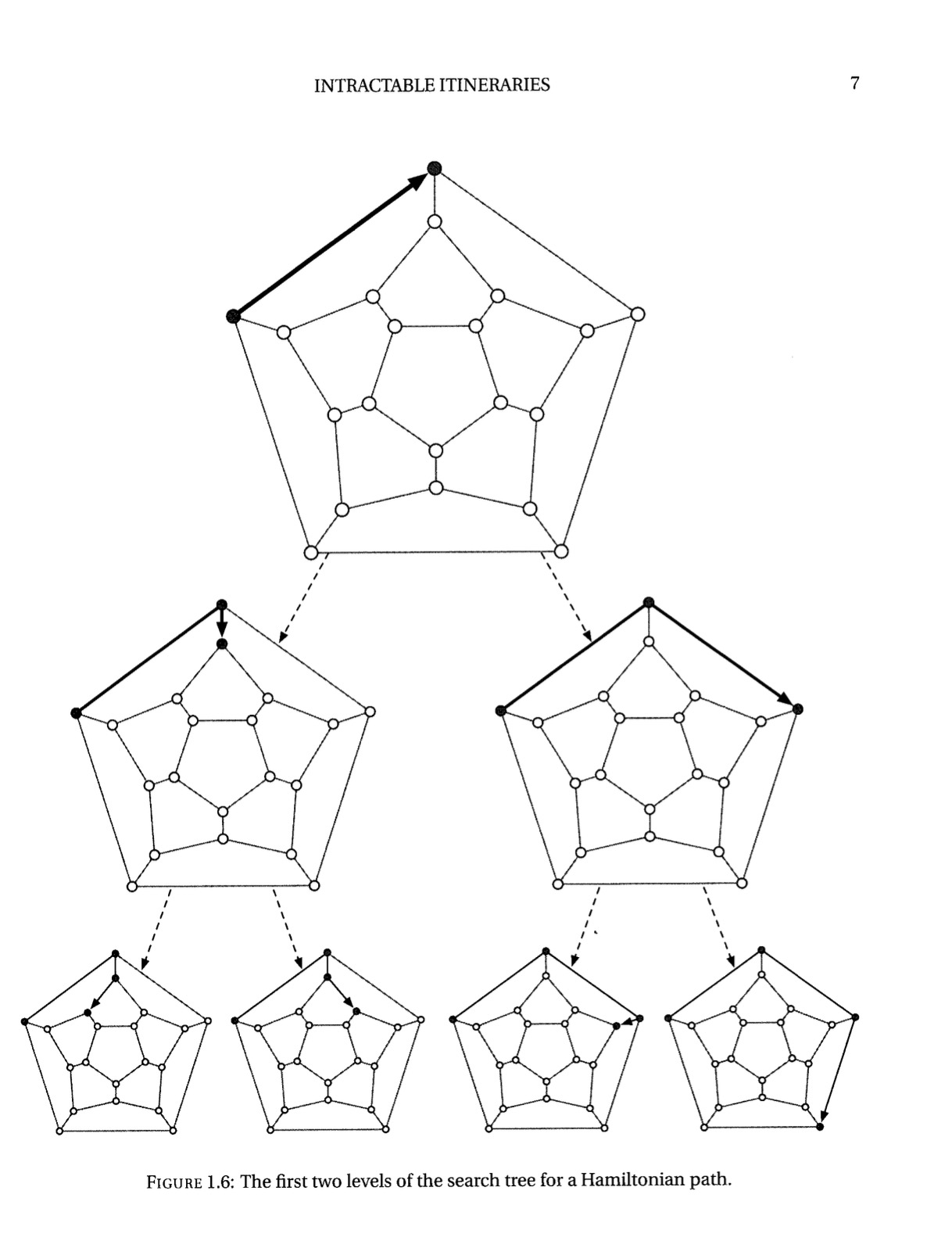
欧拉路径和汉密尔顿路径乍一看很相似，但深层次是不同的问题，首先欧拉问题讲每条路径都需要走且走一次，但是汉密尔顿问题并没有这个限制，并不关心边。其次汉密尔顿问题没有简单的规则进行判断。最坏情况需要2的n次方种。

在这里还讲了验证存在和非存在的难度不对称性。如有人想在干草堆里找针，拿出针直接看，就知道是不是，这里就像验证汉密尔顿路径，只需要看是否合法经过每一个点就可以。但是在草堆里找就需要把草堆翻一遍，就像这里需要穷尽所有。

汉密尔顿问题属于NP完全问题，现在最好的算法复杂度也是2的n次方。汉密尔顿问题的意义远超图论和问题本身，证明汉密尔顿问题的复杂性是理论计算机科学中的“圣杯”。