目录
第二章 端到端的机器学习项目
第二章是加州房价问题,很经典的问题了,这里把重要的东西总结出来就可以。
2.2.2 选择性能指标
RMSE算是经典的误差表示形式。对于较大的误差,因为平方的缘故,数值较大。
\[\operatorname{RMSE}(\mathbf{X}, h)=\sqrt{\frac{1}{m} \sum_{i=1}^m\left(h\left(\mathbf{x}^{(i)}\right)-y^{(i)}\right)^2}\]个别数值较大或有异常区域是,使用MAE(Mean Absolute Error)
\[\operatorname{MAE}(\mathbf{X}, h)=\frac{1}{m} \sum_{i=1}^m\left|h\left(\mathbf{x}^{(i)}\right)-y^{(i)}\right|\]RMSE对应欧几里得范数,也叫做$\ell_2$范数,也即是距离。记作:
\[\|\cdot\|_2\]或
\[\|\cdot\|\]MAE对应$\ell_1$范数,也称为曼哈顿范数。理解为街区移动两点间的距离。记作: \(\|\cdot\|_1\) 一般而言,包含$n$个元素的向量$v$的$\ell_k$定义为: \(\|\mathbf{v}\|_k=\left(\left|v_0\right|^k+\left|v_1\right|^k+\cdots+\left|v_n\right|^k\right)^{\frac{1}{k}}\) 性质:
- 范数指标越高,越关注大值忽略小值。
2.3 获取数据
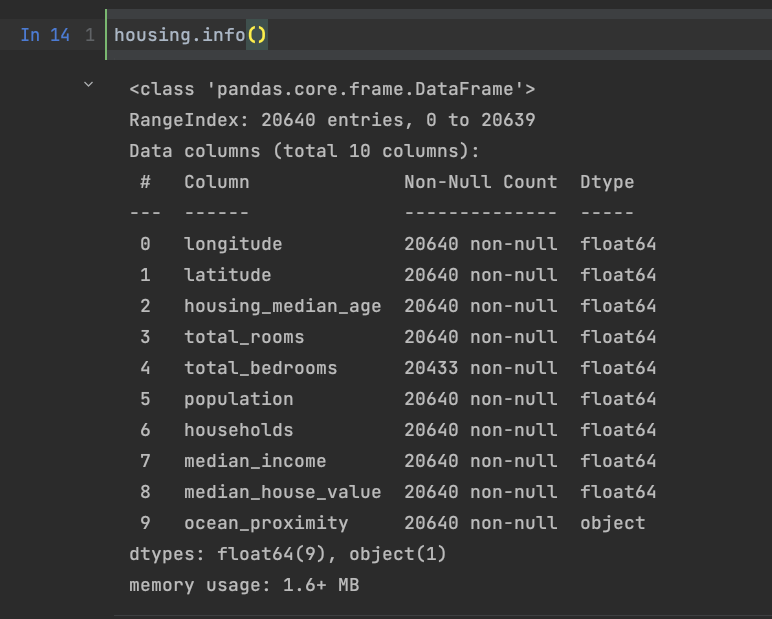
数据基本情况见上图,总共有10列数据,一共有20640个数据,其中total_bedrooms有20433个非空值,意味着有207个空值。
观察ocean_proximity中有多少种情况,使用value_counts()
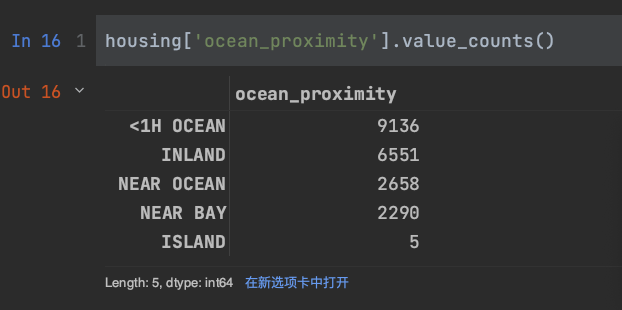
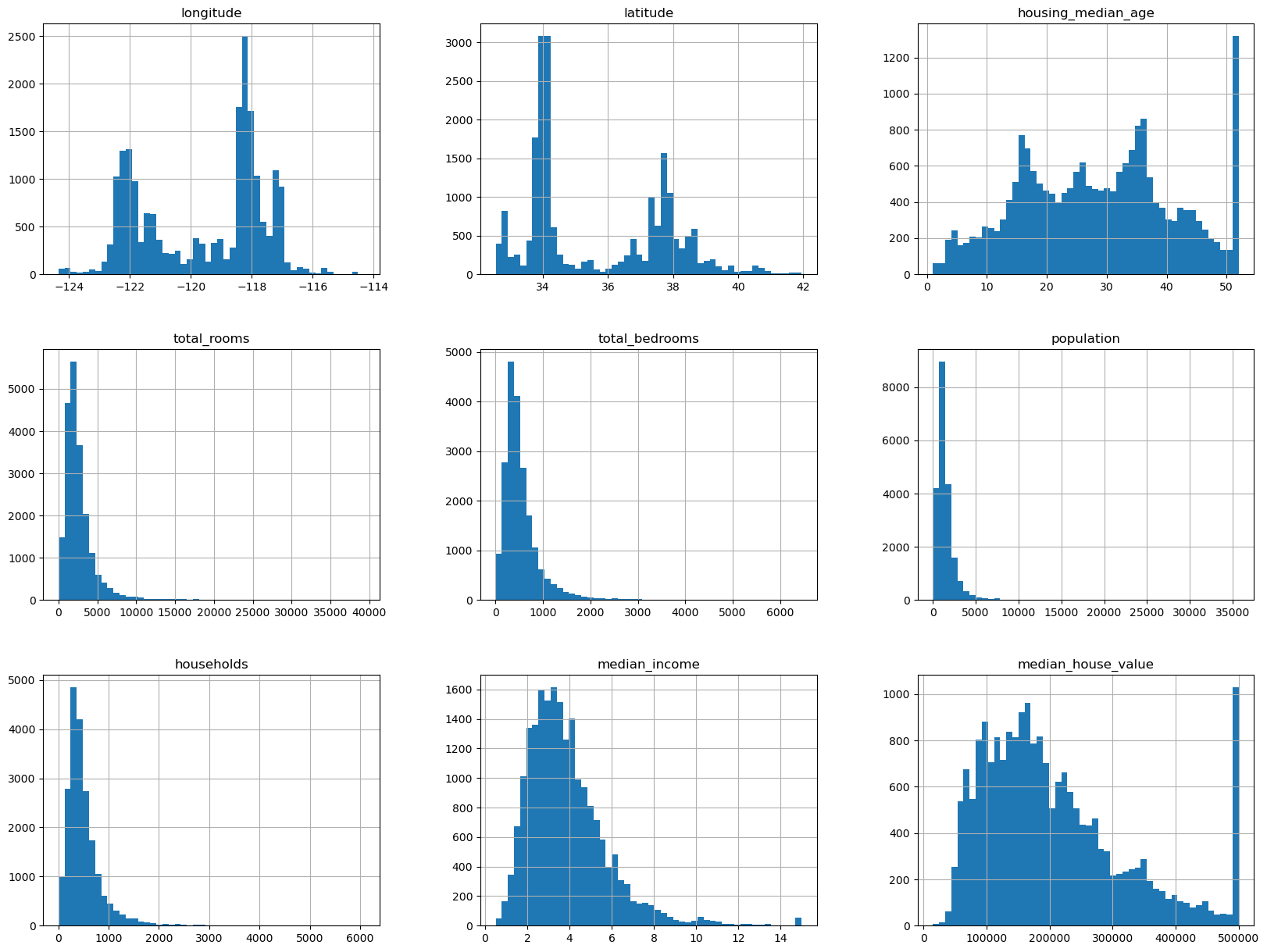
使用describe显示概要。分别画出每个属性的直方图:
2.3.4 创建测试集
``
import numpy as np
def split_train_test(data, test_ratio):
shuffled_indices = np.random.permutation(len(data))
test_set_size = int(len(data) * test_ratio)
test_indices = shuffled_indices[:test_set_size]
train_indices = shuffled_indices[test_set_size:]
return data.iloc[train_indices], data.iloc[test_indices]
``
np.random.permutation method randomly permute a sequence, or return a permuted range.If x is a multi-dimensional array, it is only shuffled along its first index.在这里的作用就是打乱标签。iloc取相应行,返回dataframe。
如果想要让每次的数据集都相同,可以在np.random.permutation前加上np.random.seed(66)。这个方法也有缺陷,其缺陷在于在数据集更新之后,还是会产生不同的结果,因此可以采用更加稳定的方式划分。常见的解决方案是让每个数据都有一个标识符,比如zlib.crc()可以计算出某个数的hash值,按照于最大值的比例来筛选出测试集。
我们也可以直接使用Scikit-Learn提供的train_test_split()函数。
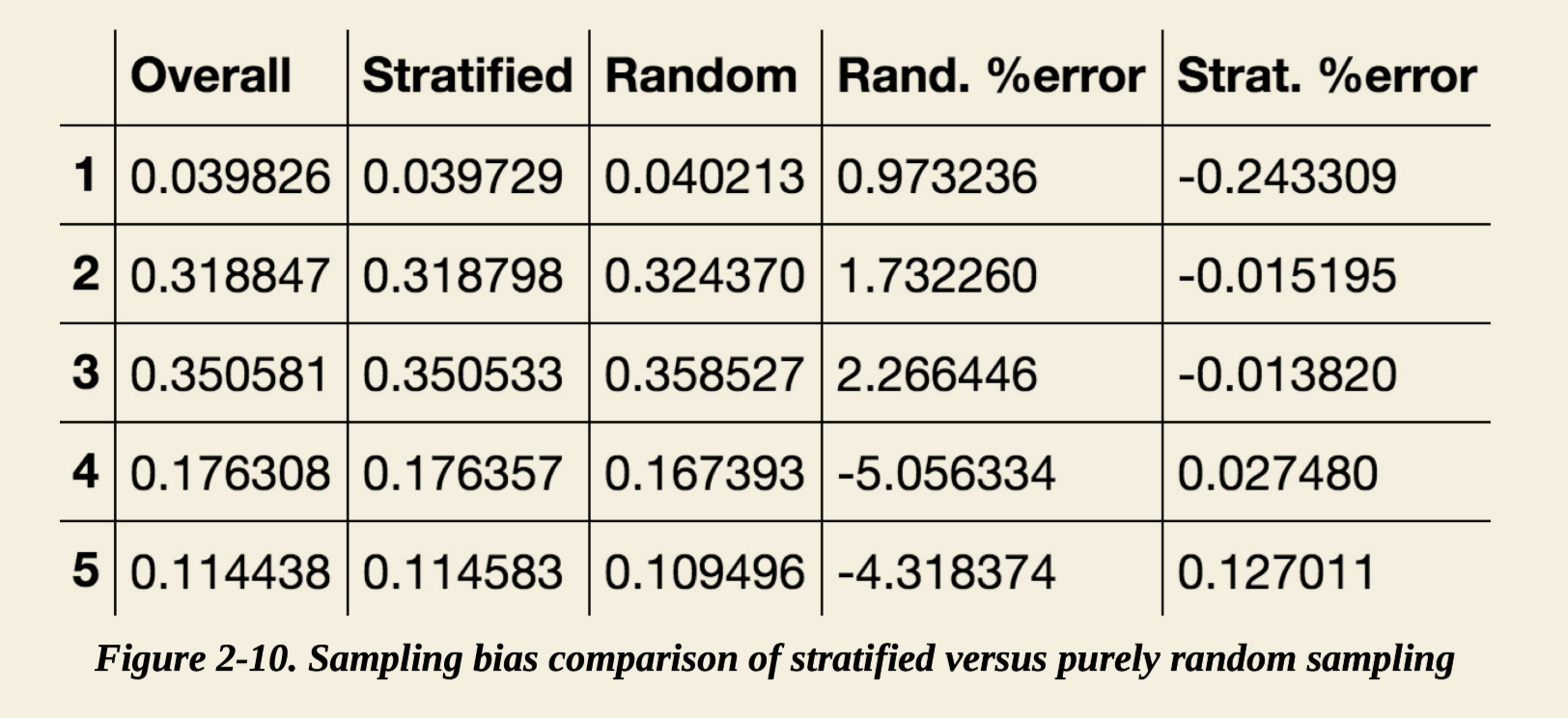
随机抽样对于大样本数据通常效果不错,但是对于样本较少的情况,往往容易产生偏差,比如调查公司找1000个人来调查,为了让这些人能代表所有人,性别分布也需要和实际情况接近。再比如测试集和数据在不同数据层级的比例要保持一致,就可以用Scikit-Learn的StratifiedShuffleSplit
2.4 数据探索及可视化
2.4.1可视化
将经度纬度绘制出来,再设置圆的半径代表人口数量,颜色代表价格。
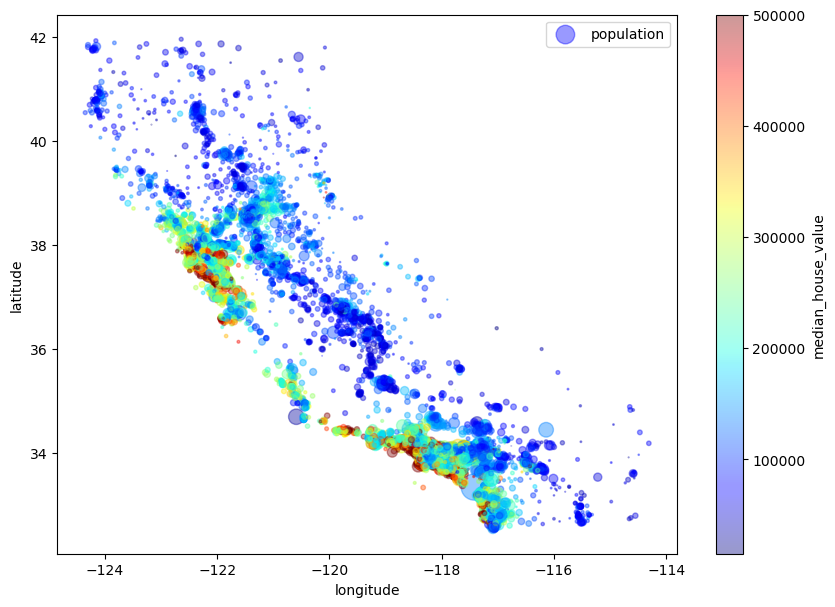
2.4.2 寻找相关性
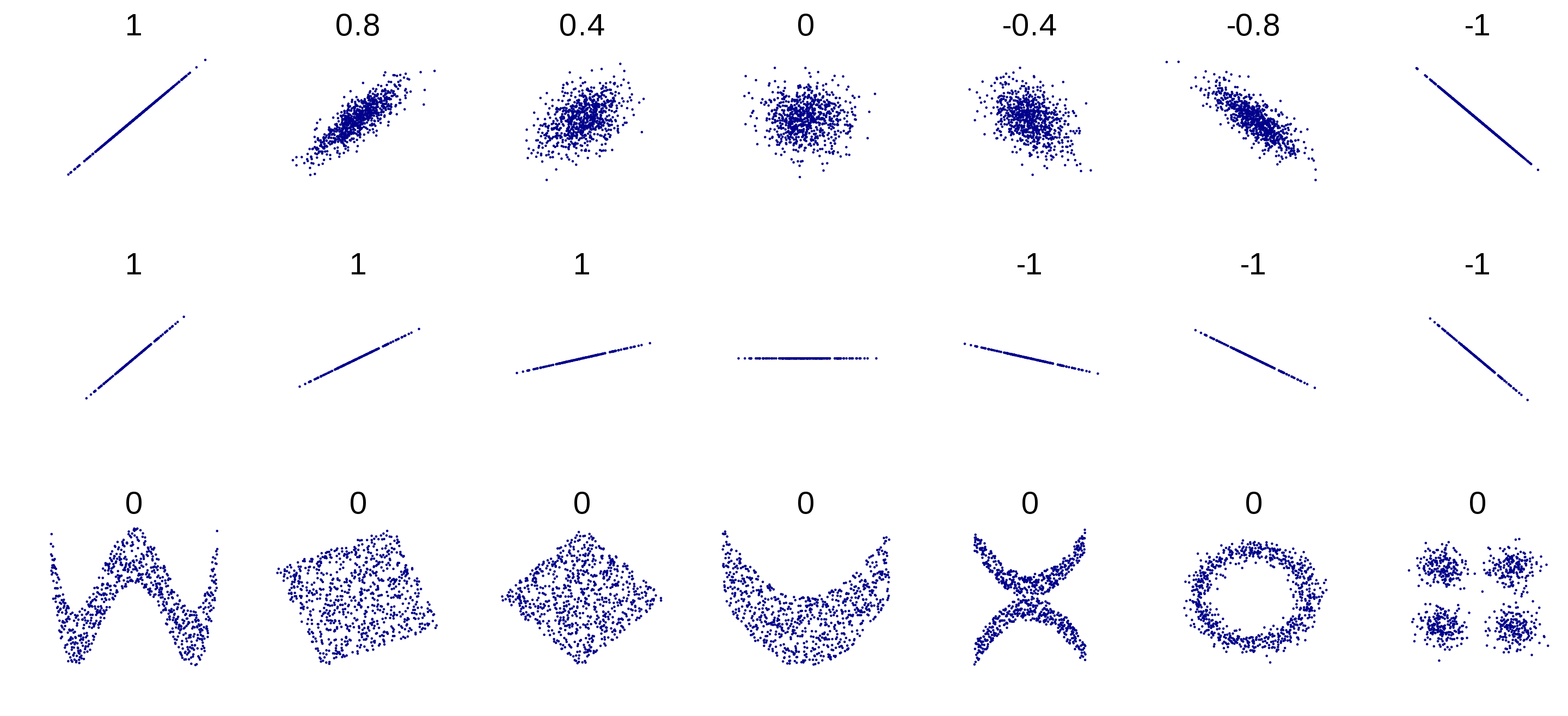
使用corr()方法可以计算出每对属性之间的相关系数。相关系数的变化由-1到1,越接近-1代表负相关,反之为正相关。相关性和斜率无关。
2.4.3 试验不同属性的组合
使用不同的组合如每个家庭的房间数。寻找相关关系。
2.5 数据准备
2.5.1 数据清理
对于缺失值的处理:
-
放弃相应区域
-
放弃整个属性
-
将缺失值设为某个值
相对应的函数:
- dropna()
- drop()
- fillna()
Scikit-Learn使用SimpleImputer类来处理缺失值。
2.5.2 处理文本和分类属性
- OridinalEncoder
- OneHotEncoder
2.5.3 自定义转换器
``
from sklearn.base import BaseEstimator, TransformerMixin
rooms_ix, bedrooms_ix, population_ix, households_ix = 3, 4, 5, 6
class CombinedAttributesAdder(BaseEstimator, TransformerMixin):
def __init__(self, add_bedrooms_per_room = True): # no *args or **kargs
self.add_bedrooms_per_room = add_bedrooms_per_room
def fit(self, X, y=None):
return self # nothing else to do
def transform(self, X, y=None):
rooms_per_household = X[:, rooms_ix] / X[:, households_ix]
population_per_household = X[:, population_ix] / X[:, households_ix]
if self.add_bedrooms_per_room:
bedrooms_per_room = X[:, bedrooms_ix] / X[:, rooms_ix]
return np.c_[X, rooms_per_household, population_per_household,bedrooms_per_room]
else:
return np.c_[X, rooms_per_household, population_per_household]
attr_adder = CombinedAttributesAdder(add_bedrooms_per_room=False)
housing_extra_attribs = attr_adder.transform(housing.values)
``
2.5.4 特征缩放
- MinMaxScaler
- StandardScaler
2.5.5 转换流水线
- Pipeline
- ColumnTransform
2.6 选择和训练模型
2.6.1 训练和评估训练集
分别使用LinearRegression 和 DecisionTree训练模型,使用RMSE进行验证发现线性模型效果很差,但是决策树的RMSE为0。真的有这么好吗?应该是出现了过拟合。
2.6.2 使用交叉验证进行评估
- 方案一:使用train_test_split()函数划分数据集和验证集进行评估。
- 方案二:使用Scikit-Learn的K-fold交叉验证。
使用cross- validation可以发现更真实的模型性能的反映。
2.7 微调模型
2.7.1 网格搜索
- 方案一:手动调整(枯燥乏味)
- 方案二:使用GridSearchCV进行搜索
2.7.2 随机搜索
网格搜索适用于参数较少的情况,因为考虑到参数组合和K-fold,总尝试次数可能会很大,因此需要引入随机搜索,RandomizedSearchCV。
2.10 练习题
1.
``
from sklearn.svm import SVR
from sklearn.model_selection import GridSearchCV
param_grid = [
{'kernel': ['linear'], 'C': [10., 30., 100., 300., 1000., 3000., 10000., 30000.0]},
{'kernel': ['rbf'], 'C': [1.0, 3.0, 10., 30., 100., 300., 1000.0],
'gamma': [0.01, 0.03, 0.1, 0.3, 1.0, 3.0]},
]
svm_reg = SVR()
grid_search = GridSearchCV(svm_reg, param_grid, cv=5, scoring='neg_mean_squared_error', verbose=2)
grid_search.fit(housing_prepared, housing_labels)
``