第六章与学习相关的技巧

本章像是一个补充，主题涉及寻找最优权重参数的最优化方法、权重参数的初始值、超参数的设定方法等。此外，为了应对过拟合，本章还将介绍权值衰减、Dropout等正则化方法，并进行实现。最后将对近年来众多研究中使用的Batch Normalization方法进行简单的介绍。

这部分推荐大家可以去看一下李宏毅老师的课，专门讲optimizer的。传送门

6.1 参数的更新

神经网络的学习的目的是找到使损失函数的值尽可能小的参数。这是寻找最优参数的问题，解决这个问题的过程称为最优化（optimization）。

在前几章中，为了找到最优参数，我们将参数的梯度（导数）作为了线索。使用参数的梯度，沿梯度方向更新参数，并重复这个步骤多次，从而逐渐靠近最优参数，这个过程称为随机梯度下降法（stochastic gradient descent），简称SGD。SGD是一个简单的方法，不过比起胡乱地搜索参数空间，也算是“聪明”的方法。这一节将给出SGD的缺点，并介绍其他优化方法。

6.1.1 探险家的故事

先打一个比方，寻找最优参数时，我们所处的状况和这位探险家一样，是一个漆黑的世界。我们必须在没有地图、不能睁眼的情况下，在广袤、复杂的地形中寻找“至深之地”。大家可以想象这是一个多么难的问题。在这么困难的状况下，地面的坡度显得尤为重要。探险家虽然看不到周围的情况，但是能够知道当前所在位置的坡度（通过脚底感受地面的倾斜状况）。于是，朝着当前所在位置的坡度最大的方向前进，就是SGD的策略。勇敢的探险家心里可能想着只要重复这一策略，总有一天可以到达“至深之地”。

6.1.2 SGD

先复习SGD：

\[W \to W - \eta \frac{\partial L}{\partial W}\]

我们写一个名为SGD的Python类。

class SGD:
  def __init__(self, lr = 0.01):
    self.lr = lr

    def update(self, params, grads):
      for key in params.keys():
        params[key] -= self.lr * grads[key]

在调用的时候，是这个样子的:

network = TwoLayerNet()
optimizer = SGD

for i in range(10000):
  ···
  x_batch, t_batch = get_mini_batch(...)
  grads = network.gradient(x_batch, t_batch)
  params = network.params
  optimizer.update(params, grads)

6.1.3 SGD的缺点

虽然SGD简单，并且容易实现，但是在解决某些问题时可能没有效率。这里，在指出SGD的缺点之际，我们来思考一下求下面这个函数的最小值的问题。

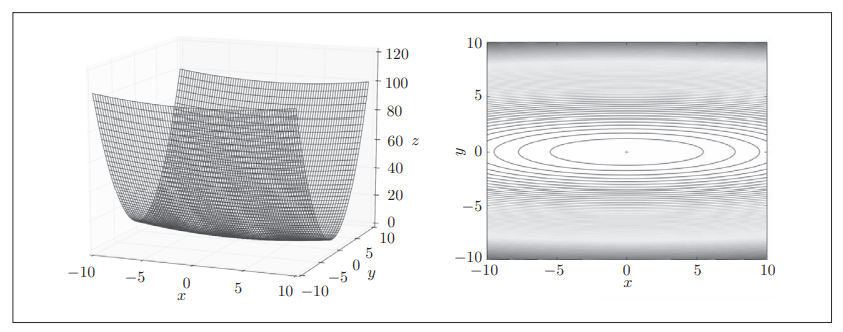
\[f(x, y) = \frac{1}{20}x^2 + y^2\]

用几张图来说明一下局限性。

第一张图，是上面函数的图像和等高线图

SGD3

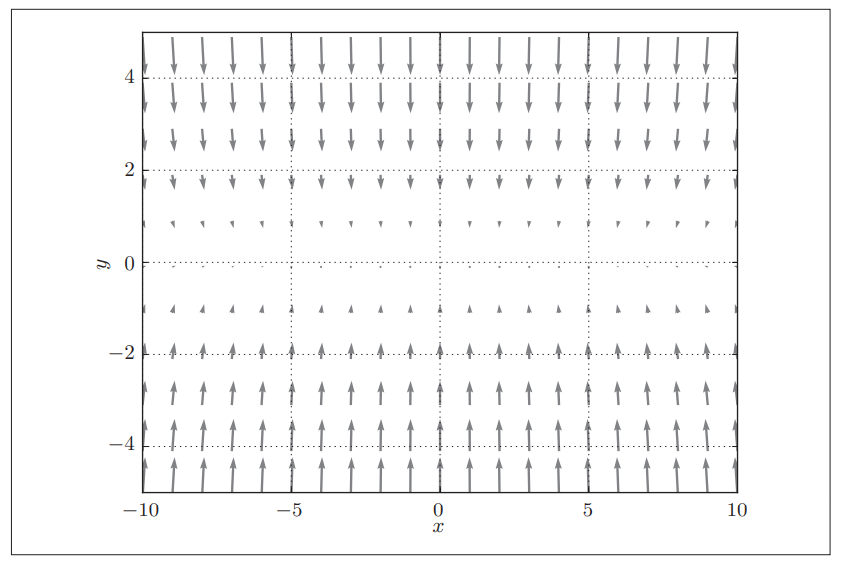
接下来是梯度方向图

SGD2

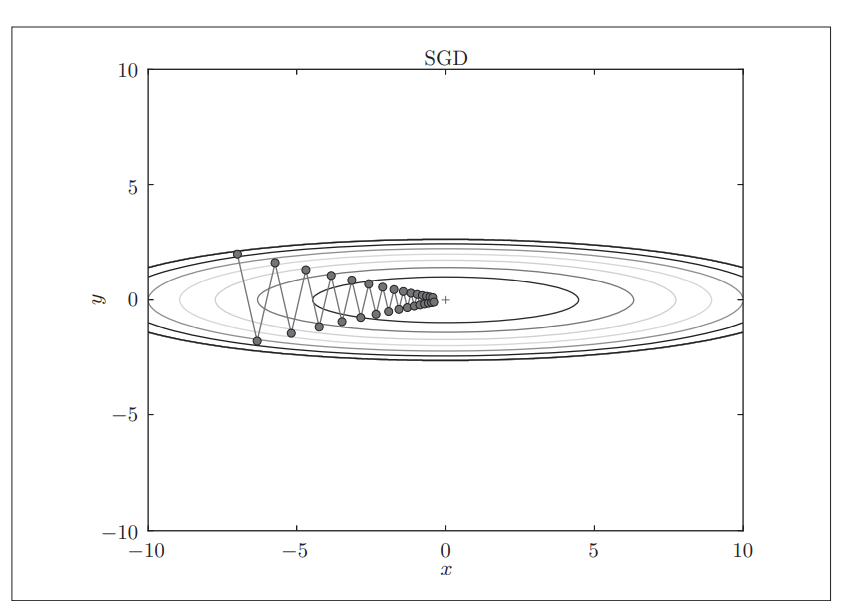
最后是从 $(x, y) = (-7.0,2.0)$ 开始的路径。

SGD1

这个路径很显然非常低效。下面将介绍取代的方法。Momentum、AdaGrad、Adam.

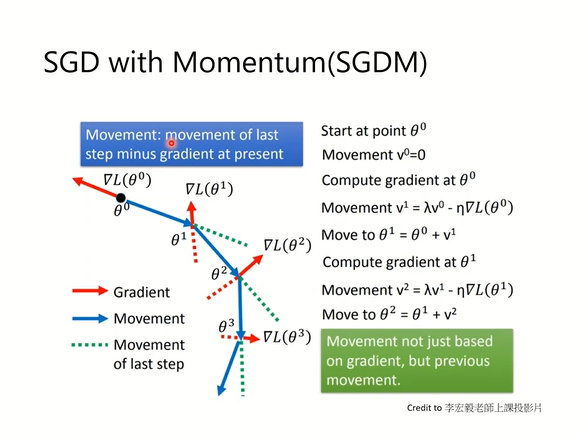
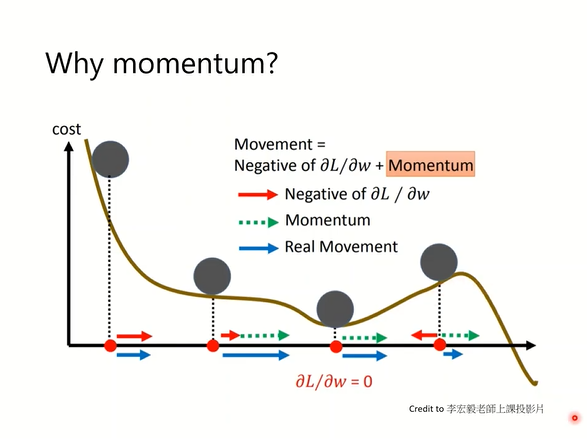
6.1.4 Momentum

Momentum 的数学表达如下：

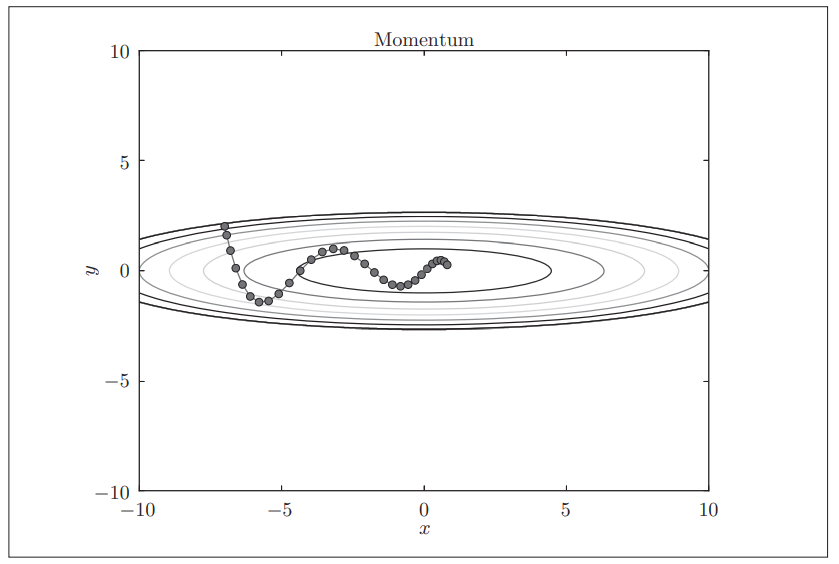
\[\upsilon \leftarrow \alpha \upsilon - \eta\frac{\partial L}{\partial W} \\ W \leftarrow W + \upsilon\]

SGD4

SGD5

更新路径就像小球在碗中滚动一样。和SGD相比，我们发现“之”字形的“程度”减轻了。这是因为虽然x轴方向上受到的力非常小，但是一直在同一方向上受力，所以朝同一个方向会有一定的加速。反过来，虽然y轴方向上受到的力很大，但是因为交互地受到正方向和反方向的力，它们会互相抵消，所以y轴方向上的速度不稳定。因此，和SGD时的情形相比，可以更快地朝x轴方向靠近，减弱“之”字形的变动程度这个应该是这么理解的，动量的存在会让当前的计算受到上一步累加的动量的影响。

最终就是这个样子：

SGD6

6.1.5 AdaGrad

在神经网络的学习中，学习率（数学式中记为 $\eta$ ）的值很重要。学习率过小，会导致学习花费过多时间；反过来，学习率过大，则会导致学习发散而不能正确进行。

在关于学习率的有效技巧中，有一种被称为学习率衰减（learning rate decay）的方法，即随着学习的进行，使学习率逐渐减小。实际上，一开始“多”学，然后逐渐“少”学的方法，在神经网络的学习中经常被使用。

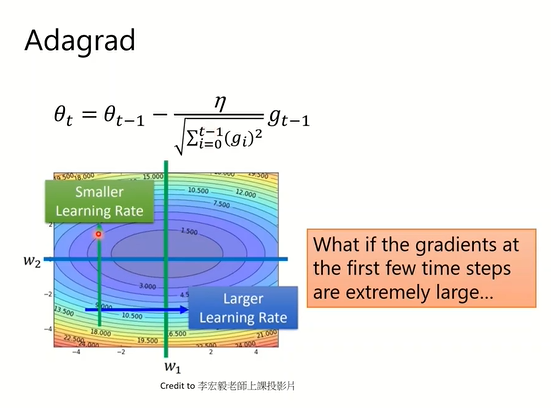
AdaGrad会为参数的每个元素适当地调整学习率，与此同时进行学习（AdaGrad的Ada来自英文单词Adaptive，即“适当的”的意思）。下面，让我们用数学式表示AdaGrad的更新方法。

\[h \leftarrow h + \frac{\partial L}{\partial W} \bigodot \frac{\partial L}{\partial W} \\ W \leftarrow W - \eta\frac{1}{\sqrt{h}}\frac{\partial L}{\partial W}\]

SGD6

就是当某一步走得太远的的时候，会调整步子小一点，大概就这个意思。

6.1.6 Adam

Adam 结合了 Momentum 和 AdaGrad 两个。

基于Adam的更新过程就像小球在碗中滚动一样。虽然Momentun也有类似的移动，但是相比之下，Adam的小球左右摇晃的程度有所减轻。这得益于学习的更新程度被适当地调整了。

6.1.7 使用哪种方法进行更新。

（目前）并不存在能在所有问题中都表现良好的方法。这4种方法各有各的特点，都有各自擅长解决的问题和不擅长解决的问题。很多研究中至今仍在使用SGD。Momentum和AdaGrad也是值得一试的方法。最近，很多研究人员和技术人员都喜欢用Adam。本书将主要使用SGD或者Adam，读者可以根据自己的喜好多多尝试。

6.2 权重的初始值

在神经网络的学习中，权重的初始值特别重要。实际上，设定什么样的权重初始值，经常关系到神经网络的学习能否成功。

6.2.1 可以将权重初始值设为0吗

如果我们把权重初始值全部设为0以减小权重的值，会怎么样呢？从结论来说，将权重初始值设为0不是一个好主意。事实上，将权重初始值设为0的话，将无法正确进行学习。

6.2.2 选择什么样的初始值

总结一下，当激活函数使用ReLU时，权重初始值使用He初始值，当激活函数为sigmoid或tanh等S型曲线函数时，初始值使用Xavier初始值。这是目前的最佳实践。

6.3 Batch Normalization

在上一节，我们观察了各层的激活值分布，并从中了解到如果设定了合适的权重初始值，则各层的激活值分布会有适当的广度，从而可以顺利地进行学习。那么，为了使各层拥有适当的广度，“强制性”地调整激活值的分布会怎样呢？实际上，Batch Normalization方法就是基于这个想法而产生的。

6.3.1 Batch Normalization 的算法

Batch Norm有以下优点。

可以使学习快速进行（可以增大学习率）。
不那么依赖初始值（对于初始值不用那么神经质）。
抑制过拟合（降低Dropout等的必要性）。

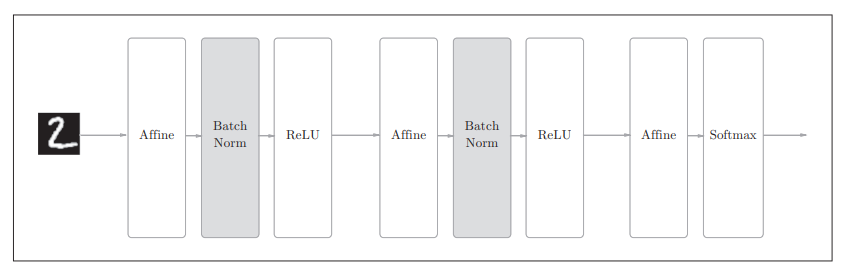
如前所述，Batch Norm的思路是调整各层的激活值分布使其拥有适当的广度。为此，要向神经网络中插入对数据分布进行正规化的层，即Batch Normalization层（下文简称Batch Norm层），如图所示。

SGD8

Batch Norm，顾名思义，以进行学习时的mini-batch为单位，按mini-batch进行正规化。具体而言，就是进行使数据分布的均值为0、方差为1的正规化。

6.3.2 Batch Normalization 的评估

我们发现，几乎所有的情况下都是使用Batch Norm时学习进行得更快。同时也可以发现，实际上，在不使用Batch Norm的情况下，如果不赋予一个尺度好的初始值，学习将完全无法进行。综上，通过使用Batch Norm，可以推动学习的进行。并且，对权重初始值变得健壮（“对初始值健壮”表示不那么依赖初始值）。Batch Norm具备了如此优良的性质，一定能应用在更多场合中。

6.4 正则化

机器学习的问题中，过拟合是一个很常见的问题。过拟合指的是只能拟合训练数据，但不能很好地拟合不包含在训练数据中的其他数据的状态。机器学习的目标是提高泛化能力，即便是没有包含在训练数据里的未观测数据，也希望模型可以进行正确的识别。我们可以制作复杂的、表现力强的模型，但是相应地，抑制过拟合的技巧也很重要。

6.4.1 过拟合

发生过拟合的原因，主要有以下两个：

模型拥有大量参数、表现力强。
训练数据少。

6.4.2 权值衰减

权值衰减是一直以来经常被使用的一种抑制过拟合的方法。该方法通过在学习的过程中对大的权重进行惩罚，来抑制过拟合。很多过拟合原本就是因为权重参数取值过大才发生的。

6.4.3 Dropout

作为抑制过拟合的方法，前面我们介绍了为损失函数加上权重的L2范数的权值衰减方法。该方法可以简单地实现，在某种程度上能够抑制过拟合。但是，如果网络的模型变得很复杂，只用权值衰减就难以应对了。在这种情况下，我们经常会使用Dropout方法。Dropout是一种在学习的过程中随机删除神经元的方法。训练时，随机选出隐藏层的神经元，然后将其删除。被删除的神经元不再进行信号的传递，如图6-22所示。训练时，每传递一次数据，就会随机选择要删除的神经元。然后，测试时，虽然会传递所有的神经元信号，但是对于各个神经元的输出，要乘上训练时的删除比例后再输出。

6.5 超参数的验证

神经网络中，除了权重和偏置等参数，超参数（hyper-parameter）也经常出现。这里所说的超参数是指，比如各层的神经元数量、batch大小、参数更新时的学习率或权值衰减等。如果这些超参数没有设置合适的值，模型的性能就会很差。虽然超参数的取值非常重要，但是在决定超参数的过程中一般会伴随很多的试错。本节将介绍尽可能高效地寻找超参数的值的方法。

超参数的最优化的内容，简单归纳一下，如下所示。

步骤0

设定超参数的范围。

步骤1

从设定的超参数范围中随机采样。

步骤2

使用步骤1中采样到的超参数的值进行学习，通过验证数据评估识别精度（但是要将epoch设置得很小）。

步骤3

重复步骤1和步骤2（100次等），根据它们的识别精度的结果，缩小超参数的范围。

6.6 小结

参数的更新方法，除了SGD之外，还有Momentum、AdaGrad、Adam等方法。
权重初始值的赋值方法对进行正确的学习非常重要。
作为权重初始值，Xavier初始值、He初始值等比较有效。
通过使用Batch Normalization，可以加速学习，并且对初始值变得健壮。
抑制过拟合的正则化技术有权值衰减、Dropout等。
逐渐缩小“好值”存在的范围是搜索超参数的一个有效方法。

第六章 与学习相关的技巧