第四章 神经网络的学习
上一章我们讲前向传播,主要说的数据的传递和计算,没有涉及到参数的训练和选择,本章的主题是神经网络的学习。为了使神经网络可以学习,引入了损失函数这个指标,学习的目的是以该损失函数为基准,找出使它的值最小的权重参数。
4.1 从数据中学习
神经网络的特征就是可以从数据中学习。所谓从数据中学习,指的就是可以由税局自动决定权重参数的值。
4.1.1 数据驱动
所谓数据驱动,强调了数据对机器学习的重要性。几乎所有的事情都和数据有关。以下列出三种解决问题的方法。
- 人面对问题时,研究问题,想出算法,最终解决问题。
- 从图中提取特征,再学习模式,最终解决问题。
- 直接学习数据,得到答案。
深度学习有时也被称为端到端机器学习(end-to-end machine learning)。
4.1.2 训练数据和测试数据
在机器学习中一般将数据集分为测试集和训练集。
4.2 损失函数
神经网络用来寻找最优权重参数的指标被称作损失函数。这个损失函数可以使用任意函数,但一半用均方误差和交叉熵误差等。
4.2.1 均方误差
用作损失函数的函数很多,其中最有名的是均方误差。(mean squared error MSE),表达形式如下:
\[E = \frac{1}{2}\sum_{k}(y_k-t_k)^2\]这里的$y_k$代表神经网络的输出,$t_k$代表监督数据,$k$代表维数。下来我们进行实现:
def mean_squared_error(y,t):
return (np.sum((y-t)**2))*0.5
观察数学意义可以知道,MSE的大小直接反映了预测结果和真实值之间的差异。
4.2.2 交叉熵误差
\[E= -\sum_kt_klog\ y_k\]公式里的$log$代表以$e$为底的自然对数($log_e$)。$y_k$是神经网络的输出,$t_k$是监督值,也就是标准值。$t_k$使用one-hot表示。
def cross_entropy_error(y,t):
delta = 1e-7
return - np.sum(t * np.log(y + delta))
因为np.log(0)会计算成负无穷,所以这里delta的作用是为了应对这个情况。
4.2.3 mini-batch学习
上一章我们讲了批处理,对应实际中使用的批处理,损失函数的写法也要做相应改变。之前介绍的损失函数考虑的都是单个数据的损失函数,如果要求所有的训练数据的损失函数的总和,以交叉熵为例,可以写成如下的形式:
\[E = -\frac{1}{N}\sum_n\sum_kt_{nk}log\ y_{nk}\]这里假设有$N$个数据,$t_nk$代表第$n$个数据的第$k$个元素的值。另外,MNIST有60000个数据,假设以全部数据为对象求损失函数的和,计算过程需要花费较长的时间。实际中的数据集比这个量更大,因此,我们从全部数据中选出一批数据,然后对每个mini-batch进行学习。这种方式叫做mini-batch学习。
之前我们已经有了读取数据集的代码,接下来我们要从中随机选取10个数据。随机选取可以使用np.random.choice()。
import sys,os
import numpy as np
sys.path.append(os.pardir)
from dataset.mnist import load_mnist
(x_train, t_train),(x_test, t_test) = load_mnist(flatten=True, normalize=True)
train_size = x_train.shape[0]
batch_size = 10
batch_mask = np.random.choice(train_size,batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
4.2.4 mini-batch 版交叉熵误差的实现
def cross_entropy_error(y,t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
delta = 1e-7
batch_size = y.shape[0]
return -np.sum(t * np.log(y + delta))/batch_size
对于非one-hot标签,可以用下面的形式:
def cross_entropy_error(y,t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
delta = 1e-7
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
4.2.5 为何要设定损失函数
原因主要有以下几点:
- 不能关注某一个特定的参数
- 不能以识别精度为指标
- 识别精度对微小的参数变化不敏感
4.3 数值微分
4.3.1 导数
4.3.2 数值微分的例子
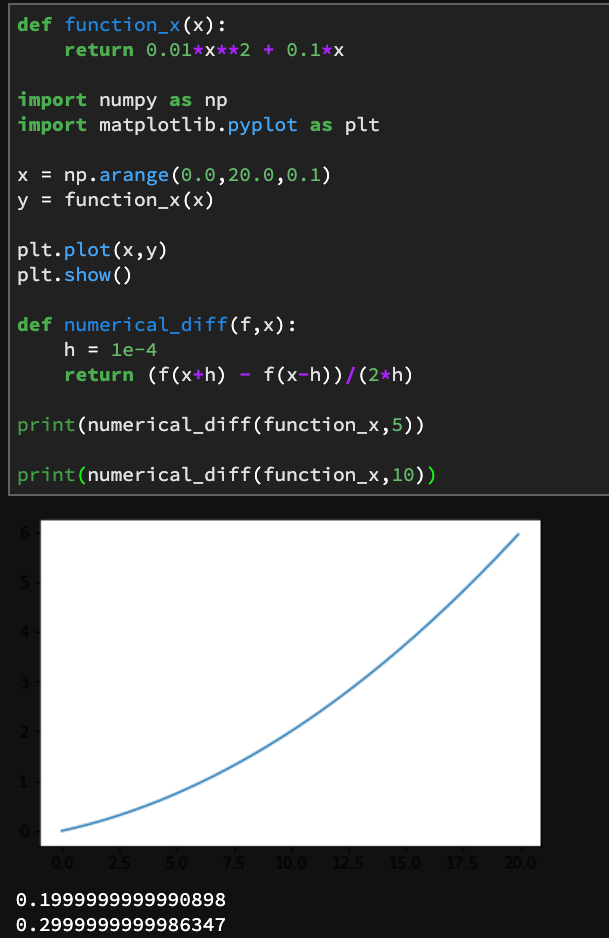
下面的例子是一个求数值微分的例子。使用的中心差分。求的是$f(x) = 0.01x^2+0.1x$在$f(x+h)$到$f(x-h)$之间的差分。
def function_x(x):
return 0.01*x**2 + 0.1*x
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0.0,20.0,0.1)
y = function_x(x)
plt.plot(x,y)
plt.show()
def numerical_diff(f,x):
h = 1e-4
return (f(x+h) - f(x-h))/(2*h)
print(numerical_diff(function_x,5))
print(numerical_diff(function_x,10))
4.3.3 偏导数
这里以一个函数为例:
\[f(x_0,x_1) = x_0^2 + x_1^2\]因为这里有两个变量,所以求偏导数时,固定一个值,对另一个变量求导数。
4.4 梯度
学习了导数和偏导数,那么什么是梯度呢。形如$ (\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial x_1}) $的由全部变量的偏导数汇总而成形成的向量被称为梯度。
下面实际看一个例子:
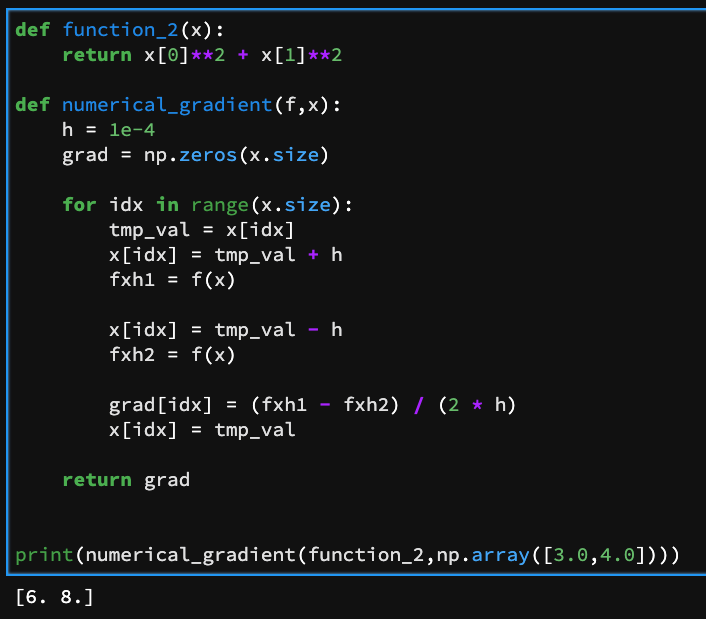
def function_2(x):
return x[0]**2 + x[1]**2
def numerical_gradient(f,x):
h = 1e-4
grad = np.zeros(x.size)
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = tmp_val + h
fxh1 = f(x)
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2 * h)
x[idx] = tmp_val
return grad
print(numerical_gradient(function_2,np.array([3.0,4.0])))
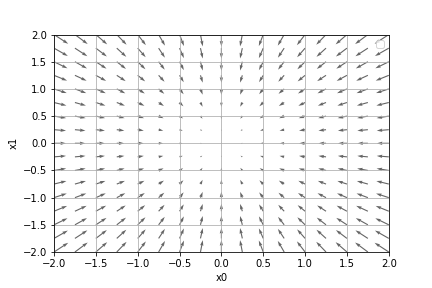
这里提供一个梯度的可视化方法。使用了matplotlib中的quiver函数。quiver函数使用方法很简单,前面四个参数分别代表了箭头起点,XY,也就是每一个点的梯度位置,后两个参数就是计算出的梯度,代表箭头在两个方向上的矢量。
x0 = np.arange(-2, 2.5, 0.25)
x1 = np.arange(-2, 2.5, 0.25)
X, Y = np.meshgrid(x0, x1)
X = X.flatten()
Y = Y.flatten()
grad = numerical_gradient(function_2, np.array([X, Y]) )
plt.figure()
plt.quiver(X, Y, -grad[0], -grad[1], angles="xy",color="#666666")#,headwidth=10,scale=40,color="#444444")
plt.xlim([-2, 2])
plt.ylim([-2, 2])
plt.xlabel('x0')
plt.ylabel('x1')
plt.grid()
plt.legend()
plt.draw()
plt.show()
4.4.1 梯度法
讲解了梯度的意义,现在要讲的是具体的使用,也就是梯度法对于寻找最优参数的意义。这里的最优参数就是损失函数取最小值时的参数。
但是这个最小值通常是很难找的,因为函数通常比较复杂,并且可能找到的仅仅是局部最优解,但是不可否认的是,梯度的下降方向是可以使损失函数减小的方向。
简而言之,梯度法就是通过不断的沿着梯度方向前进,逐渐减小损失函数的值的过程就叫做梯度法。寻找最小值的方法乘坐梯度下降法,反之,则称为梯度上升法。
接下来用数学方式表示梯度法。
\[x_0= x_0-\eta\frac{\partial{f}}{\partial{x_0}}\] \[x_1= x_0-\eta\frac{\partial{f}}{\partial{x_1}}\]在上面的式子里,$\eta$称为学习率(learning rate)。这个类似于步长的概念。学习率需要事先确定,过大或者过小都不利于找到好的位置。
接下来实现一下梯度下降法。
def gradient_decent(f,init_x,lr=0.01,step_num=100):
x = init_x
for i in range(step_num):
grad = numerical_gradient(f,x)
x = x - lr*grad
return x
拥有了所有的工具,接下来尝试解决问题。
问题:用梯度法求解$f(x_0,x_1) = x_0^2+x_1^2$的最小值。
思路:使用梯度下降,指定一个初始值,学习率和步长即可。下面是代码和图示。
# coding: utf-8
import numpy as np
import matplotlib.pylab as plt
def numerical_gradient(f, X):
if X.ndim == 1:
return _numerical_gradient_no_batch(f, X)
else:
grad = np.zeros_like(X)
for idx, x in enumerate(X):
grad[idx] = _numerical_gradient_no_batch(f, x)
return grad
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
x_history = []
for i in range(step_num):
x_history.append( x.copy() )
grad = numerical_gradient(f, x)
x -= lr * grad
return x, np.array(x_history)
def function_2(x):
return x[0]**2 + x[1]**2
init_x = np.array([-3.0, 4.0])
lr = 0.1
step_num = 20
x, x_history = gradient_descent(function_2, init_x, lr=lr, step_num=step_num)
plt.plot( [-5, 5], [0,0], '--b')
plt.plot( [0,0], [-5, 5], '--b')
plt.plot(x_history[:,0], x_history[:,1], 'o')
plt.xlim(-3.5, 3.5)
plt.ylim(-4.5, 4.5)
plt.xlabel("X0")
plt.ylabel("X1")
plt.savefig('gradient_decent_visualization.png')
plt.show()
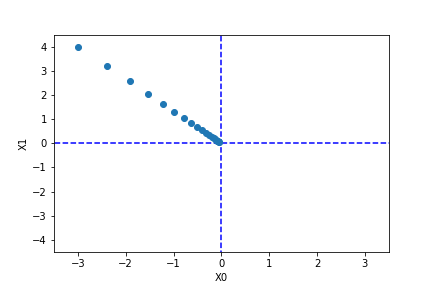
像学习率这样的参数,取大取小都不好,他和诸如权重和偏置这样通过神经网络学习获得的参数不同,它需要人为进行设定,这一类参数通常被称为超参数。
4.4.2 神经网络的梯度
神经网络的学习过程也需要求梯度,这里的损失函数就是基于权重参数的梯度。如有一个形状为$2 \times 3$的权重为$W$的神经网络,损失函数用$L$表示,此时梯度可以用 $\frac{\partial{L}}{\partial{W}}$ 表示。
\[W = \begin{pmatrix} \omega_{11}&\omega_{12}&\omega_{13} \\ \omega_{21}&\omega_{22}&\omega_{23} \end{pmatrix}\] \[\frac{\partial{L}}{\partial{W}} = \begin{pmatrix} \frac{\partial{L}}{\partial{\omega_{11}}}&\frac{\partial{L}}{\partial{\omega_{12}}}&\frac{\partial{L}}{\partial{\omega_{13}}} \\ \frac{\partial{L}}{\partial{\omega_{21}}}&\frac{\partial{L}}{\partial{\omega_{22}}}&\frac{\partial{L}}{\partial{\omega_{23}}} \end{pmatrix}\]$\frac{\partial{L}}{\partial{W}}$ 的元素是关于$W$的偏导数,例如第一行第一列的元素 $\frac{\partial{L}}{\partial{\omega_{11}}}$ 表示当 $\omega_{11}$ 稍微变化时,损失函数$L$会发生多大变化。接下来看每一个简单神经网络求梯度的例子:
import numpy as np
def softmax(x):
exp_a = np.exp(x-np.max(x))
sum_exp_a = np.sum(exp_a)
return exp_a/sum_exp_a
def cross_entropy_error(y,t):
delta = 1e-7
return -np.sum(t*np.log(y + delta))
class SimpleNet:
def __init__(self):
self.W = np.random.randn(2,3)
def predict(self,x):
return np.dot(x,self.W)
def loss(self,x,t):
z = self.predict(x)
y = softmax(z)
loss = cross_entropy_error(y,t)
return loss
net = SimpleNet()
x = np.array([0.6,0.9])
p = net.predict(x)
print(p)
print(np.argmax(p))
t = np.array([1,0,0])
loss = net.loss(x,t)
print(loss)
上面构建了简单的神经网络,使用交叉熵作为损失函数。求得了误差之后,接下来使用梯度下降,更新参数后看误差的变化。
4.5 学习算法的实现
截至目前,神经网络学习的所有基础知识已经全部讲解完毕。接下来确认一下神经网络的学习步骤。
前提
神经网络存在合适的权重的偏置,调整权重和偏置的过程称为学习。
步骤1(mini-batch) 从训练数据中选取一部分数据,使用这部分数据来减小损失函数的值。
步骤2(计算梯度)
为了减小损失函数的值,需要求出各个权重参数的梯度。梯度表示损失函数的值减小最多的方向。
步骤3(更新参数) 将权重参数做微小的更新。
步骤4(重复)
重复上面的步骤
神经网络的学习按照上面的步骤进行,这里的数据是随机选择的mini batch数据,所以称为随机梯度下降法(stochastic gradient descent)。因此随机梯度下降法也叫做“对随机选择的数据进行的梯度下降法”,在很多框架中,随机梯度下降法一般由一个名为SGD的函数实现。
下面以手写数字识别为例做实现。
4.5.1 2层神经网络的类
我们将这个类命名为TwoLayerNet的类。这个类用于构建我们所用的神经网络,使用这个类可以根据需要创建。
def sigmoid(x):
return 1/(1+np.exp(-x))
def softmax(x):
exp_x = np.exp(x-np.max(x))
sum_exp_x = np.sum(exp_x)
return exp_x/sum_exp_x
def cross_entropy_error(y,t):
delta = 1e-7
return -np.sum(t * np.log/(y + delta))
class TwoLayerNet:
def __init__(self,input_size,hidden_size,output_size):
self.params = {}
self.params['W1'] = np.random.randn(input_size,hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = np.random.randn(hidden_size,output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
def loss(self,x,t):
y = self.predict(x)
return cross_entropy_error(y,t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis = 1)
t = np.argmax(t, axis = 1)
accuracy = np.sum(y == t)/float(x.shape[0])
return accuracy
def numerical_gradient(self, x, t):
loss_W = lambda W:self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W1'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
这个类的实现稍稍有点长,但是并没有什么新鲜的内容。TwoLayerNet类有params和grads两个字典实例变量,在实现的时候,调用了构造函数,init(self,input_size,hidden_size,output_size)第一个参数代表输入层神经元个数,第二个参数代表隐藏层的神经元个数,第三个参数代表输出层神经元个数,在这里,输入层的神经元个数为 $28 \times 28 = 784$,输出为10个类别,隐藏层设置一个合适的参数即可。 在后面将会详细讨论参数初始化问题,这里我们使用符合高斯分布的随机数进行初始化,偏置使用0进行初始化。predict(self, x)和 accuracy(self, x, t)的实现和上一章的神经网络的推理处理基本一样。如 果仍有不明白的地方,请再回顾一下上一章的内容。另外,loss(self, x, t)是计算损失函数值的方法。这个方法会基于predict()的结果和正确解标签,计算交叉熵误差。剩下的numerical_gradient(self, x, t)方法会计算各个参数的梯度。根 据数值微分,计算各个参数相对于损失函数的梯度。另外,gradient(self, x, t) 是下一章要实现的方法,该方法使用误差反向传播法高效地计算梯度。
4.5.2 mini-batch的实现
神经网络的学习使用的是前面介绍过的mini batch学习,所谓mini batch学习指的是从训练数据中随机选取一部分数据,再使用这些数据用梯度法更新参数。
import numpy as np
from mnist import load_mnist
def numerical_gradient(f, X):
if X.ndim == 1:
return _numerical_gradient_no_batch(f, X)
else:
grad = np.zeros_like(X)
for idx, x in enumerate(X):
grad[idx] = _numerical_gradient_no_batch(f, x)
return grad
def cross_entropy_error(y,t):
delta = 1e-7
return -np.sum(t*np.log(y + delta))
def _numerical_gradient_no_batch(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 还原值
return grad
(x_train,t_train),(x_test,t_test) = load_mnist(normalize=True,one_hot_label=True)
train_loss_list = []
#超参数
iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
network = TwoLayerNet(input_size=x_train.shape[1],hidden_size=50,output_size=10)
for i in range(iters_num):
print(i)
batch_mask = np.random.choice(train_size,batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
grad = network.numerical_gradient(x_batch,t_batch)
for key in ('W1','b1','W2','b2'):
print(key)
network.params[key] -= learning_rate * grad[key]
loss = network(x_batch,t_batch)
train_loss_list.append(loss)
print(loss)
这样的计算是十分缓慢的。以至于,在计算的时候。完成整个循环需要很久很久。
4.5.3 基于测试数据的评价
从上面的代码,可以看出,使用梯度下降法,实现了损失函数减小。 在神经网络的学习中,必须首先确认是否发生过拟合,即能否识别除训练数据以外的数据。接下来要确认的是神经网络是否掌握泛化能力。
4.6 小结
本章介绍了神经网络的学习。首先,为了顺利进行神经网络的学习,我们导入损失函数这个指标。以这个损失函数为基准,找出使它的值达到最小的权重参数,这就是神经网络的学习目标。为了找到尽可能小的损失函数值,我们介绍了使用函数斜率的梯度法。
- 机器学习中使用的数据集分为训练数据和测试数据
- 神经网络用训练数据进行学习,并用测试数据评价学习到的模型的泛化能力。
- 神经网络的学习以损失函数为指标,更新权重参数,以使损失函数的值减小
- 利用某个给定的微小值的差分求倒数的过程,称为数值微分
- 利用数值微分,可以计算权重参数的梯度
- 数值为分虽然费时间,但是实现起来很简单。下一章中要实现的是复杂一些的误差反向传播法,可以高速的计算梯度。