第三章 神经网络
3.6 手写数字识别
上一个post介绍了神经网络的基本内容,这一节搭配项目解决实际问题。这个例子非常简单,是一个机器学习里的Hello world。手写数字识别问题。但是这个例子是不完全的,我们假设学习已经全部完成,我们用学习到的参数,先实现神经网络的“推理处理”。这也叫神经网络的前向传播。
3.6.1 MNIST数据集
这个数据集网上的资料实在太多了,就连他的进阶版本Fashion MNIST也出来很久了,相信能看到现在的人没有太多人不知道这个数据集。
介绍简单带过。MNIST数据集(Mixed National Institute of Standards and Technology database)是美国国家标准与技术研究院收集整理的大型手写数字数据库,包含60,000个示例的训练集以及10,000个示例的测试集。
MNIST的图像是28 $\times$ 28像素的灰度图像(1通道),像素的取值在0到255之间。每个图像都标有对应的阿拉伯数字标签。
这本书提供了数据集和相应的代码。传送门
import sys,os
sys.path.append(os.pardir)
from dataset.mnist import load_mnist
(x_train, t_train),(x_test, t_test) = load_mnist(flatten=True, normalize=False)
print(x_train.shape)
print(t_train.shape)
print(x_test.shape)
print(t_test.shape)
第一次执行代码可能比较慢,原因是需要下载,服务器在国外,下载的比较慢。也可以手动下载放在文件夹,我就是用的这个方法(自动下载实在太慢了)。
于是我们打印出训练集,测试集和对应的label的shape。
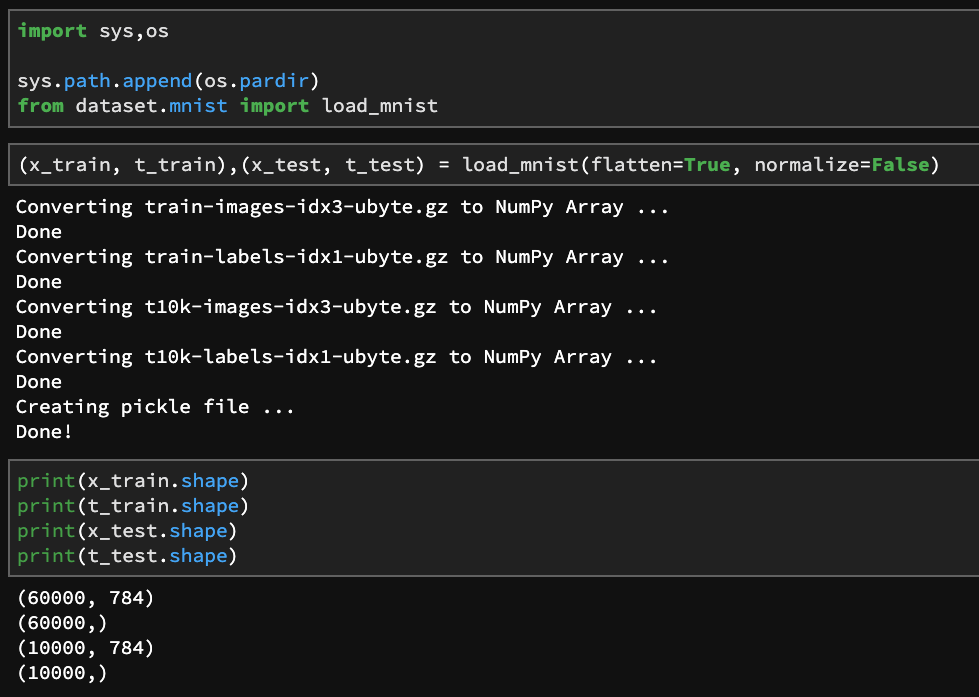
这里对代码做一点简单说明,这里的load_mnist函数是将数据集做导入,分别为两个训练集两个测试集,flatten参数为True代表将28 $\times$ 28的图像扁平化,变成1 $\times$ 784的向量。normalize的含义是将数值标准化为0到1之间的数字,这个函数还可以传入一个参数,就是one_hot_label,这个参数设置为True将会让标签变为one hot representation。
因为这里并不涉及参数的训练,因此我们需要导入参数,这离有一个pkl文件,保存着训练好的参数,直接导入就可以。下来简单显示一下图片。
import sys,os,cv2
import numpy as np
sys.path.append(os.pardir)
from dataset.mnist import load_mnist
(x_train, t_train),(x_test, t_test) = load_mnist(flatten=True, normalize=True)
print(x_train.shape)
print(t_train.shape)
print(x_test.shape)
print(t_test.shape)
first_image = x_train[0]
first_label = t_train[0]
print(first_label)
img = first_image.reshape(28,28)
cv2.imshow('img',img)
cv2.waitKey(0)
cv2.destroyAllWindows()

3.6.2 神经网络的推理处理
根据之前的内容,我们设计的神经网络的输入层的神经元个数,应该是784,也就是图像拉长之后的向量长度。输出层为10个神经元,因为输出层神经元的数量应该和分类的种类相等。另外,这神经网络有两个隐藏层,第一个隐藏层50个神经元,第二个有100个神经元。结合之前学过的知识,得到代码如下。
import sys,os,cv2,pickle
import numpy as np
sys.path.append(os.pardir)
from dataset.mnist import load_mnist
def sigmoid(x):
return 1/(1+np.exp(-x))
def softmax(x):
exp_x = np.exp(x-np.max(x))
sum_exp_x = np.sum(exp_x)
return exp_x/sum_exp_x
def get_data():
(x_train, t_train),(x_test, t_test) = load_mnist(flatten=True, normalize=True)
return x_test,t_test #没有训练阶段,因此只取测试数据
def init_network():
with open("sample_weight.pkl",'rb') as f:
network = pickle.load(f)
return network
def predict(network,x):
W1,W2,W3 = network['W1'],network['W2'],network['W3']
b1,b2,b3 = network['b1'],network['b2'],network['b3']
a1 = np.dot(x,W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1,W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2,W3) + b3
y = softmax(a3)
return y
x,t = get_data()
accuracy_cnt = 0
for i in range(len(x)):
y = predict(network,x[i])
p = y.argmax()
if p == t[i]:
accuracy_cnt += 1
accuracy = accuracy_cnt/t.shape[0]
print(accuracy)
最后得到的正确率为93.52%。
3.6.3 批处理
上面就是神经网络的实现,但是在实际写代码的过程中,有一个问题,那就是在计算正确率的时候,我们是一遍一遍调用predict函数,得到结果和label进行比较,使用了for循环,这显然是不好的,我们引入矩阵运算就是为了应对这样的情况。但是还应该注意到的是,我们也不能一次将所有的数据输入进去,因为这会引起内存的溢出等等一系列问题,因此我们使用批处理可以让计算更加高效。之前计算时,矩阵大小的传递过程如下:
\[[1\times784]\times[784\times50]\times[50\times100]\times[100\times10]\]下面我们一次性传入100张图片,也就是输入矩阵的大小改变,变成如下的形式。
\[[100\times784]\times[784\times50]\times[50\times100]\times[100\times10]\]通过比较可以明显的看出,一次可以计算100张图片,输出100个结果。具体的细节就不多讲了,直接上实现。
import sys,os,cv2,pickle
import numpy as np
sys.path.append(os.pardir)
from dataset.mnist import load_mnist
def sigmoid(x):
return 1/(1+np.exp(-x))
def softmax(x):
exp_x = np.exp(x-np.max(x))
sum_exp_x = np.sum(exp_x)
return exp_x/sum_exp_x
def get_data():
(x_train, t_train),(x_test, t_test) = load_mnist(flatten=True, normalize=True)
return x_test,t_test #没有训练阶段,因此只取测试数据
def init_network():
with open("sample_weight.pkl",'rb') as f:
network = pickle.load(f)
return network
def predict(network,x):
W1,W2,W3 = network['W1'],network['W2'],network['W3']
b1,b2,b3 = network['b1'],network['b2'],network['b3']
a1 = np.dot(x,W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1,W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2,W3) + b3
y = softmax(a3)
return y
x,t = get_data()
batch_size = 100
accuracy_cnt = 0
for i in range(0,len(x),batch_size):
x_batch = x[i:i+batch_size]
y_batch = predict(network,x_batch)
p = np.argmax(y_batch,axis=1)
accuracy_cnt += np.sum(p == t[i:i+batch_size])
accuracy = accuracy_cnt/t.shape[0]
print(accuracy)
最终得到的结果是完全一样的。
3.7 小结
第三章讲的是神经网络的前向传播。也就是数据是如何传递的,当然这一章的内容也是不完整的,因为没有训练部分,而是直接载入参数。
- 实现部分主要的重点在于对批处理的理解。