第三章 神经网络

紧接着第二章的内容，我们开始介绍神经网络。上一章感知机的参数都是我们认为验证给定的，对于神经网络来说，一个重要的性质就是可以自动地从数据中学习到合适的权重参数。

3.1 从感知机到神经网络

3.1.1 神经网络的例子

下图就是一个神经网络的例子，把最左边的一列称为输入层，中间一列称为中间层，中间层有时又称为隐藏层，最右边一列称为输出层。

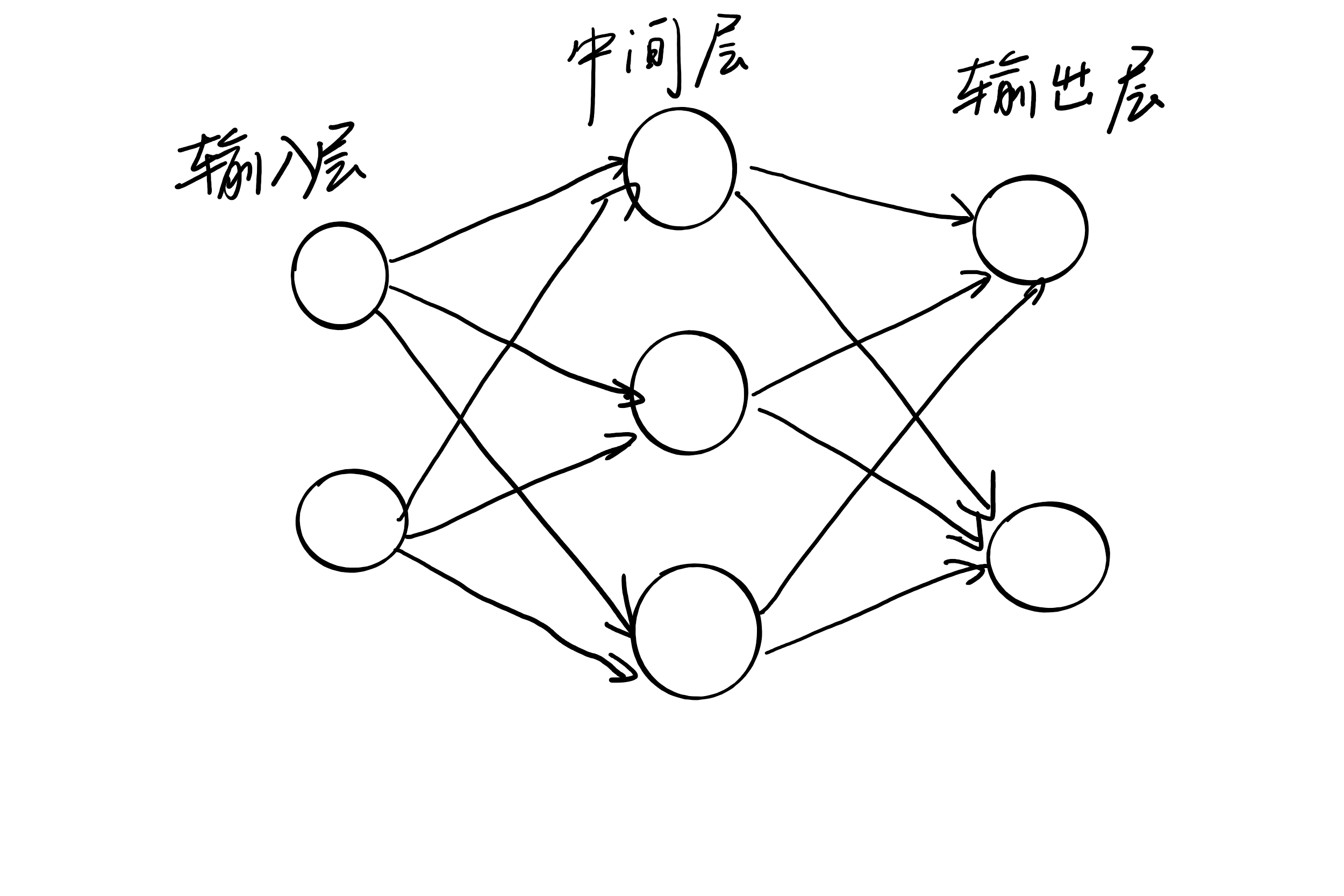
神经网络结构

按之前的习惯，我们把输入层称为第0层，隐藏层称为第1层，输出层称为第二层，因此在这里我们称之为两层神经网络。注意，也有些地方将其称为三层神经网络。但怎么叫都无伤大雅。上图的结构和之前感知机的结构很相似。那么他们有什么异同呢。

3.1.2 复习感知机

先回顾一下感知机的结构。

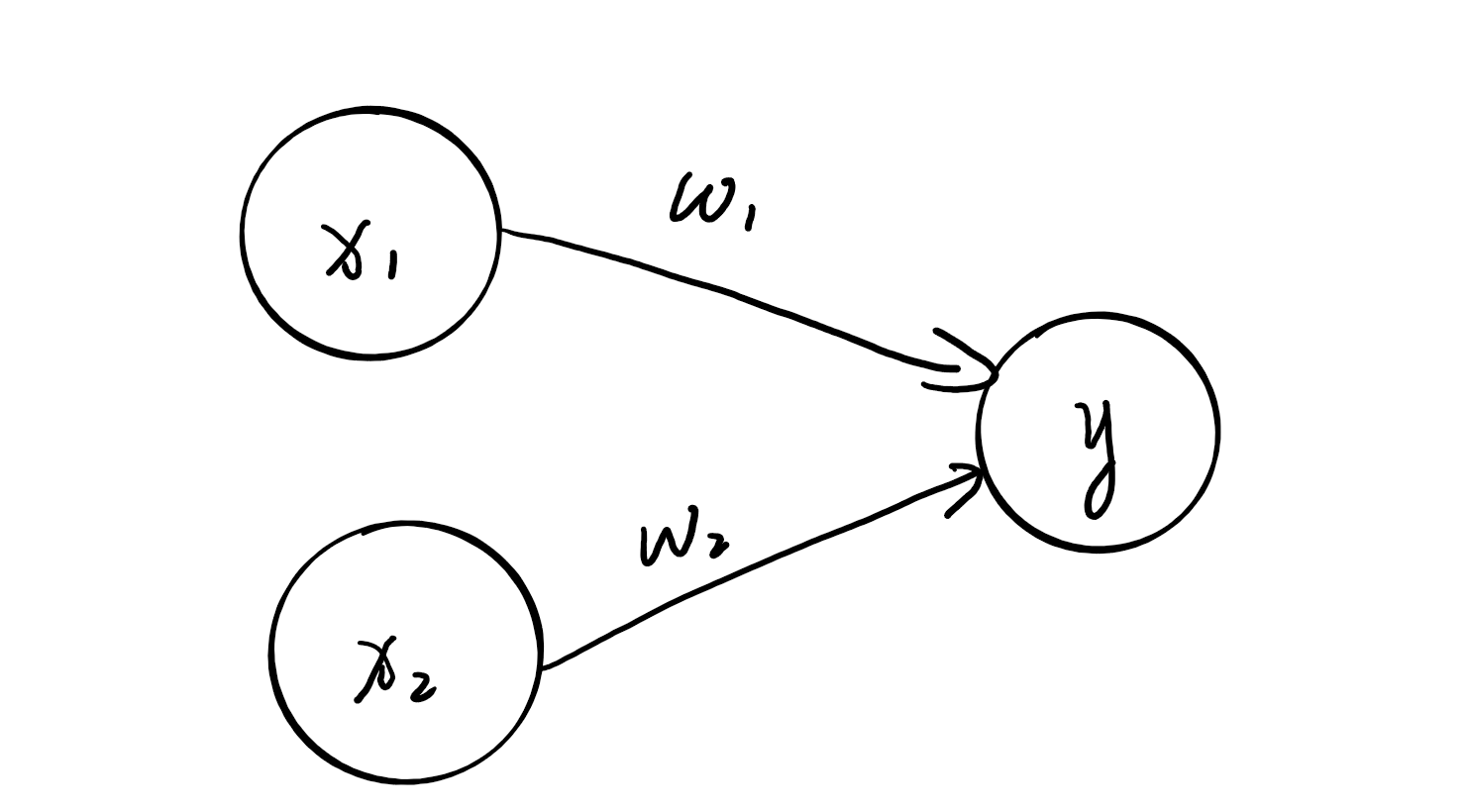
感知机的结构

感知机接收$x_1$,$x_2$两个输入信号，输出$y$，数学表达如下：

\[y=\left\{\begin{array}{ll} 0 & \left(b+w_{1} x_{1}+w_{2} x_{2} \leqslant 0\right) \\ 1 & \left(b+w_{1} x_{1}+w_{2} x_{2}>0\right) \end{array}\right.\]

$b$称为偏置，控制神经元被激活的难易程度，而$\omega_1$和$\omega_2$称为权重，表示信号的重要程度。我们发现，在上图中并没有表现出偏置，我们可以做一点小小的修改，改动后的结构如下图所示：

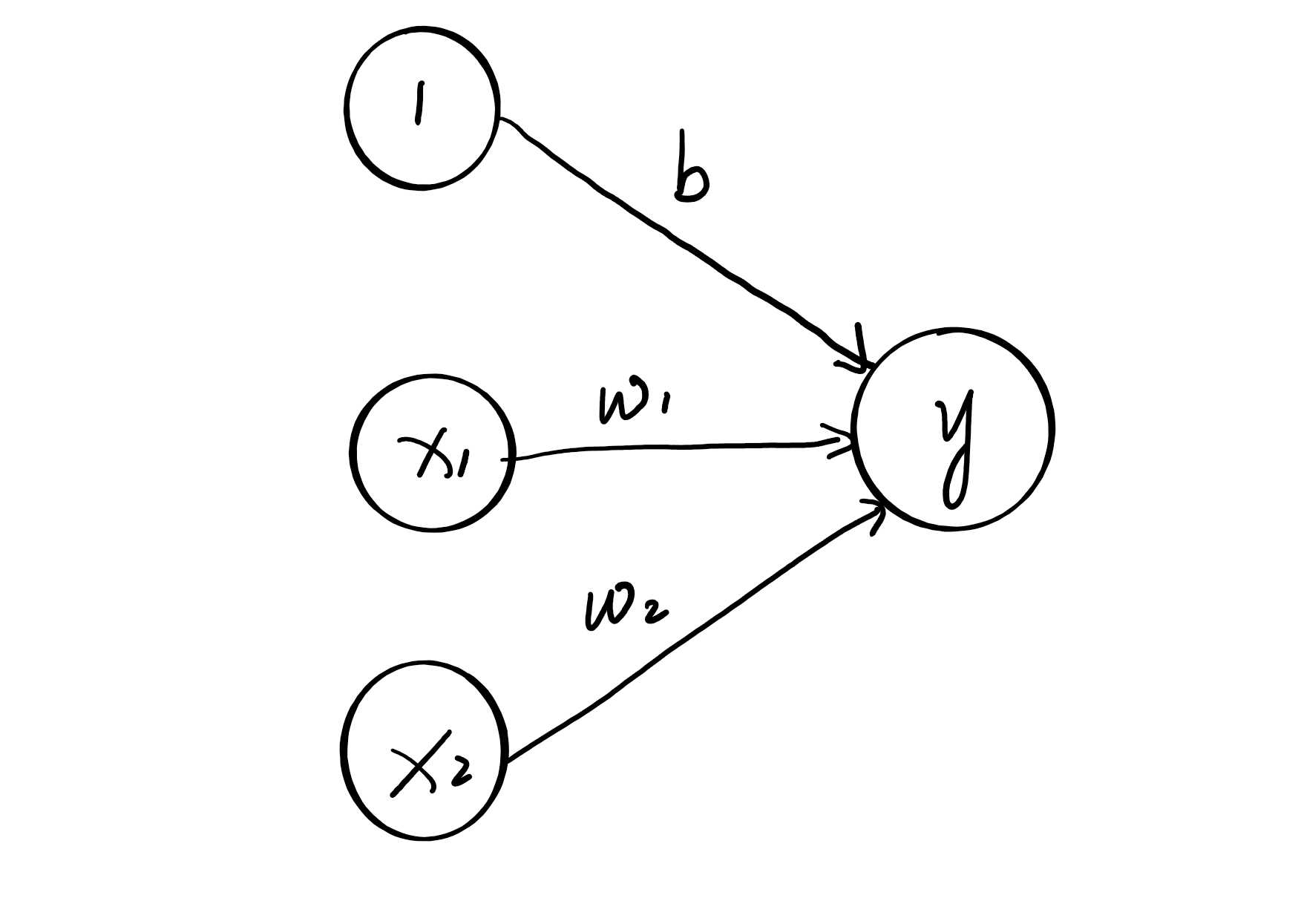
感知机带偏置的表示

在上面的表示方法中，分了两种情况来表示，表示起来并不是很方便，因此我们将原来的公式改写成下面的式子:

\[y = h(b+\omega_1x_1+\omega_2x_2)\] \[h=\left\{\begin{array}{ll} 0 & \left(x \leqslant 0 \right) \\ 1 & \left(x > 0\right) \end{array}\right.\]

3.1.3 激活函数

上面的$h(x)$函数将输入信号的总和转换为输出信号，这种函数一般称为激活函数，顾名思义，激活函数用来决定如何激活信号。 我们将上面的公式写的更详细一点：

\[a=b+\omega_1x_1+\omega_2x_2\] \[y = h(a)\]

首先计算加权输入信号和偏执的总和，记为$a$，然后激活函数$h()$，将$a$转换为输出$y$。为了明确表示这个过程，我们得到了下面的图：

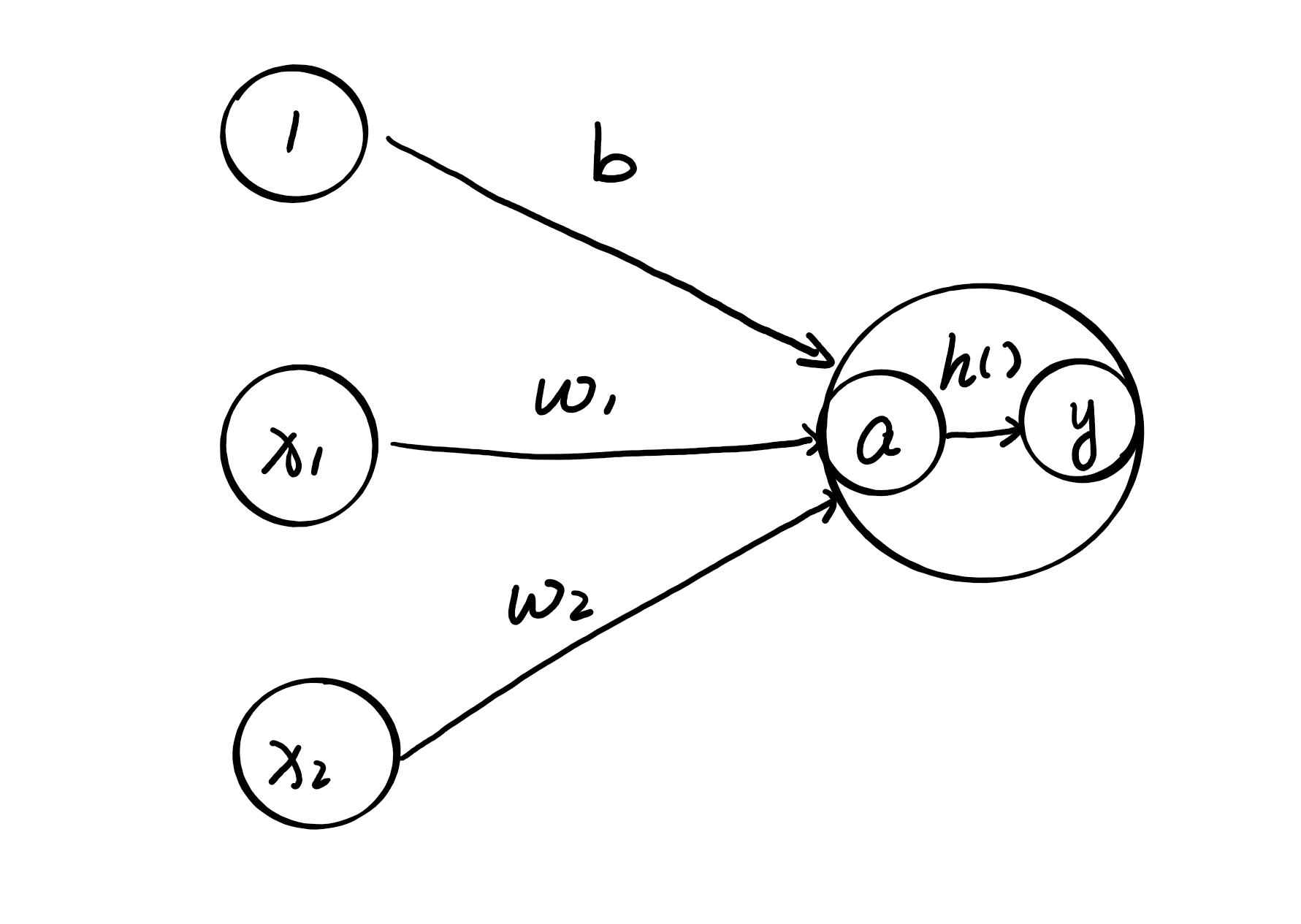
感知机详细

3.2 激活函数

下来我们详细介绍激活函数，激活函数以阈值为界，一旦超过阈值，就切换输出，这样的函数被称为阶跃函数。感知机使用了阶跃函数，那么选择其他函数会怎么样呢。

3.2.1 sigmoid函数

这是非常常见的激活函数。

\[h(x)=\frac{1}{1+e^{-x}}\]

神经网络使用sigmoid作为激活函数。神经网络和感知机的主要区别就在于激活函数。

3.2.2 阶跃函数的实现

即：

\[h=\left\{\begin{array}{ll} 0 & \left(x \leqslant 0 \right) \\ 1 & \left(x > 0\right) \end{array}\right.\] 

def step_function(x):
	if x>0:
		return 1
	else:
		return 0

这是一个最基本的实现，但是输入不能以数组的形式呈现，下面我们修改一下使之可以使用Numpy数组实现。

def step_function(x):
	y = x > 0
	
	return y.astype(np.int)

这里函数中的第二个行对输入的numpy数组判断是否大于零，大于零的返回True，反之则为False。astype将布尔值转换为整形，True变为1，False变为0。

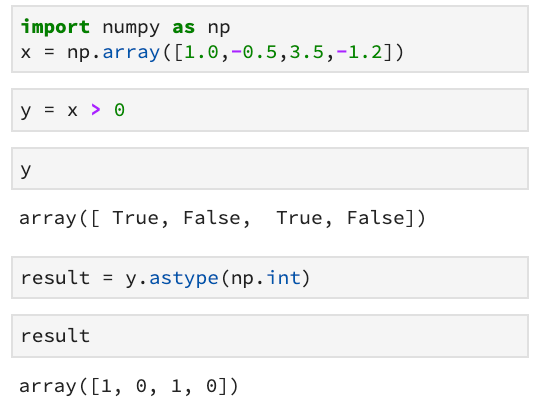
代码验证结果

3.2.3 阶跃函数的图形

我们用matplotlib来画图。

import numpy as np
import matplotlib.pyplot as plt

def step_function(x):
    return np.array(x>0,dtype=np.int)

x = np.arange(-5.0,5.0,0.1)
y = step_function(x)

plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()

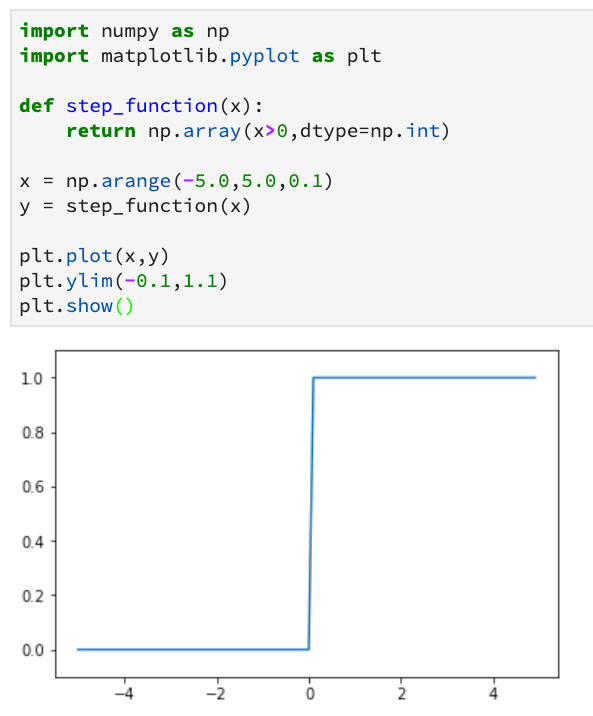
执行结果如下： 阶跃函数图像

3.2.4 sigmoid函数的实现


def sigmoid(x):
	return 1/(1+np.exp(-x))

绘图：

import numpy as np
import matplotlib.pyplot as plt

def sigmoid_function(x):
    return 1/(1+np.exp(-x))

x = np.arange(-5.0,5.0,0.1)
y = sigmoid_function(x)

plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()

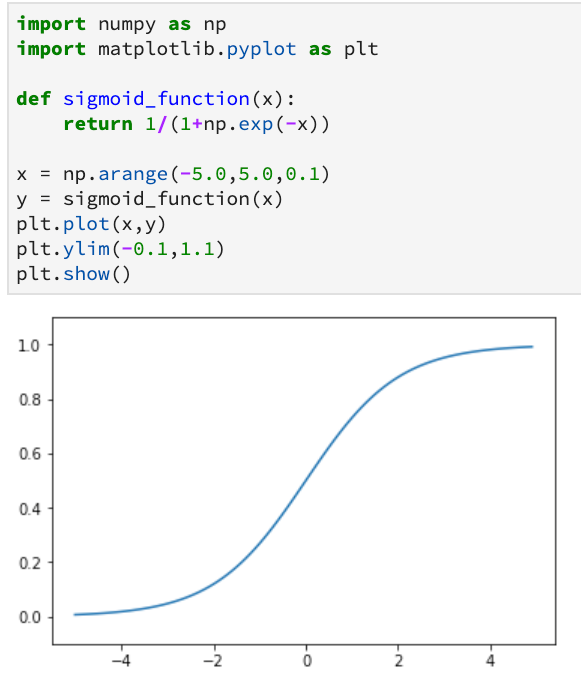
执行结果如下： sigmoid函数图像

将他们放在一起做一个对比：

import numpy as np
import matplotlib.pyplot as plt

def sigmoid_function(x):
    return 1/(1+np.exp(-x))

x = np.arange(-5.0,5.0,0.1)
y = sigmoid_function(x)
z = step_function(x)
plt.plot(x,y)
plt.plot(x,z,'--')
plt.ylim(-0.1,1.1)
plt.show()

图像对比

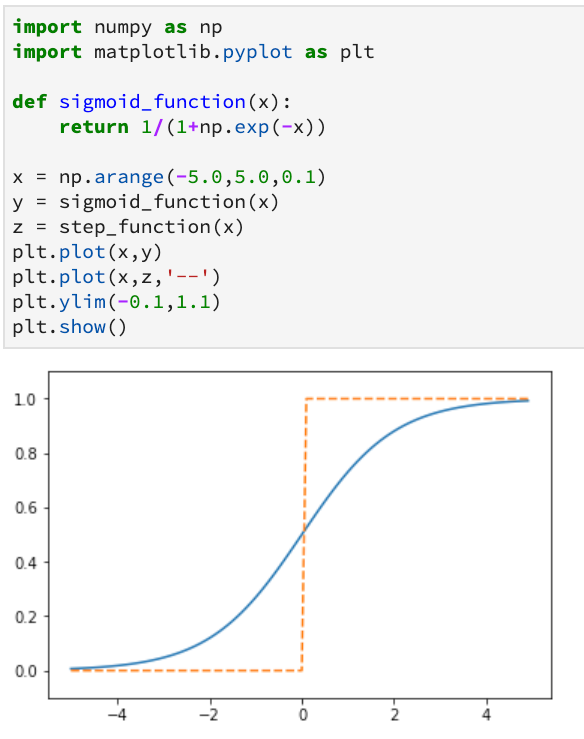
通过上图观察，他们之间究竟有什么不同。我讲这些不同归纳为以下两点：

  • sigmoid函数更加平滑，阶跃函数以0为界发生阶跃。
  • 阶跃函数只能返回0和1，sigmoid函数返回连续的值

3.2.6 非线性函数

刚刚说过的阶跃函数和sigmoid函数都是非线性函数，因为他们不是一条直线。对于神经网络来说，激活函数必须使用非线性函数。否则神经网络具有的层的概念就没有意义了 。

在这里举一个简单的例子。假设我们在这里用线性函数$h(x) = cx$为激活函数。于是$y(x)=h(h(h(x)))$作为三层神经网络的运算，于是得到$y(x)=c^3x$，我们让$c^3=a$,于是有$y(x)=ax$,这个三层网络可以用一层网络代替，那么这个三层网络就没有意义了且无论多少层都可用一层代替。

3.2.7 ReLU函数

sigmoid函数很早就开始使用了，现在使用较多的是ReLU函数(Rectified Linear Unit)。ReLU函数也很简单，输入大于0时，直接输出该值，否则输出0。可表示为：

\[h= \left\{\begin{array}{ll} 0 & \left(x \leqslant 0 \right) \\ x & \left(x > 0\right) \end{array}\right.\]

代码实现如下：

def relu(x):
	if x>0:
		return x
	else:
		return 0

def relu(x):
	return np.maxium(0,x)

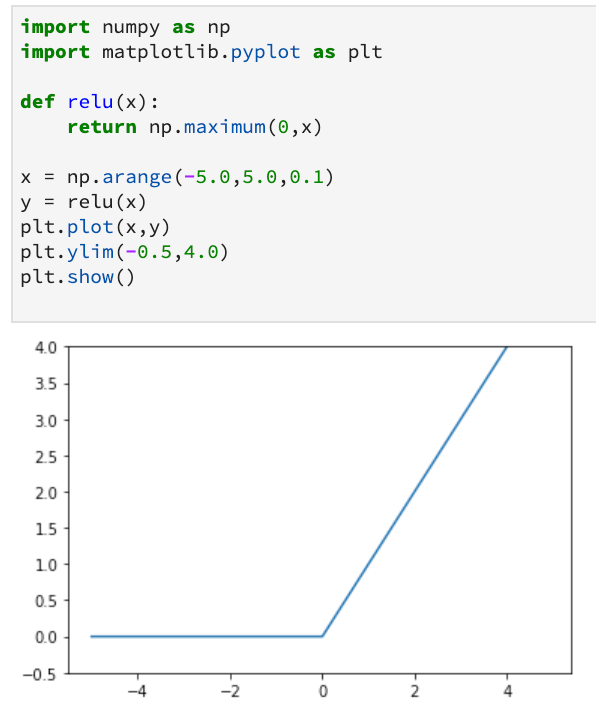
ReLU函数的图像如下。

import numpy as np
import matplotlib.pyplot as plt

def relu(x):
    return np.maximum(0,x)

x = np.arange(-5.0,5.0,0.1)
y = relu(x)
plt.plot(x,y)
plt.ylim(-0.5,4.0)
plt.show()

relu函数图像

3.3 多位数组的运算

这一部分主要是矩阵乘法的部分，包括多维数组和矩阵乘法等知识。就不再赘述了。

3.3.3 神经网络的内积

现在我们使用Numpy来实现神经网络。下面的神经网络省略了偏置和激活函数，只有权重。

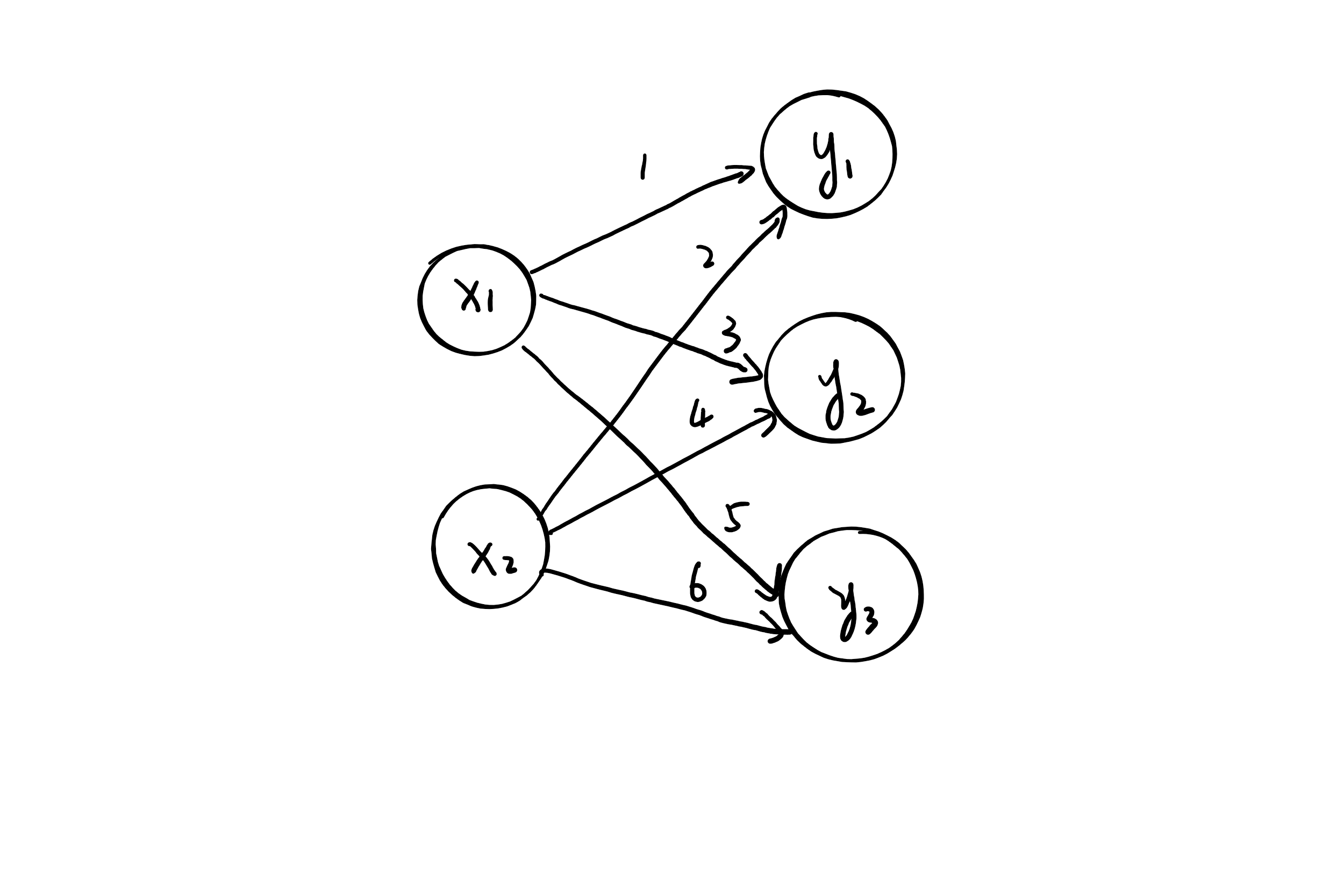
简单神经网络结构

结合上面的图，我们得到几个式子。

\[h=\left\{\begin{array}{ll} 1 \times x_1+2 \times x_2 = y_1 \\ 3 \times x_1+4 \times x_2 = y_2 \\ 5 \times x_1+6 \times x_2 = y_3 \end{array}\right.\]

使得$X = \begin{pmatrix} x_1
x_2 \end{pmatrix}$,使得$Y = \begin{pmatrix} y_1
y_2
y_3 \end{pmatrix}$ 于是有：

\[\begin{pmatrix} 1&2 \\ 3&4\\ 5&6 \end{pmatrix} \begin{pmatrix} x_1\\ x_2 \end{pmatrix} = \begin{pmatrix} y_1\\ y_2\\ y_3 \end{pmatrix}\]

在实现的时候要特别注意矩阵的维度。下面进行实现：

import numpy as np

def NLP_simple(x1,x2):
    X = np.array([[x1],[x2]])
    W = np.array([[1,2],[3,4],[5,6]])
    Y = np.dot(W,X)
    return Y


Y = NLP_simple(1,2)

NLP代码运行结果

在这里是一个简单的例子，但是应该注意到的是，当神经元个数增大时，相应的只是矩阵的大小发生了变化，也是使用矩阵的乘法完成计算。

3.4 3层神经网络的实现

我们再进一步计算更复杂的神经网络。先看下面3层神经网络的结构：

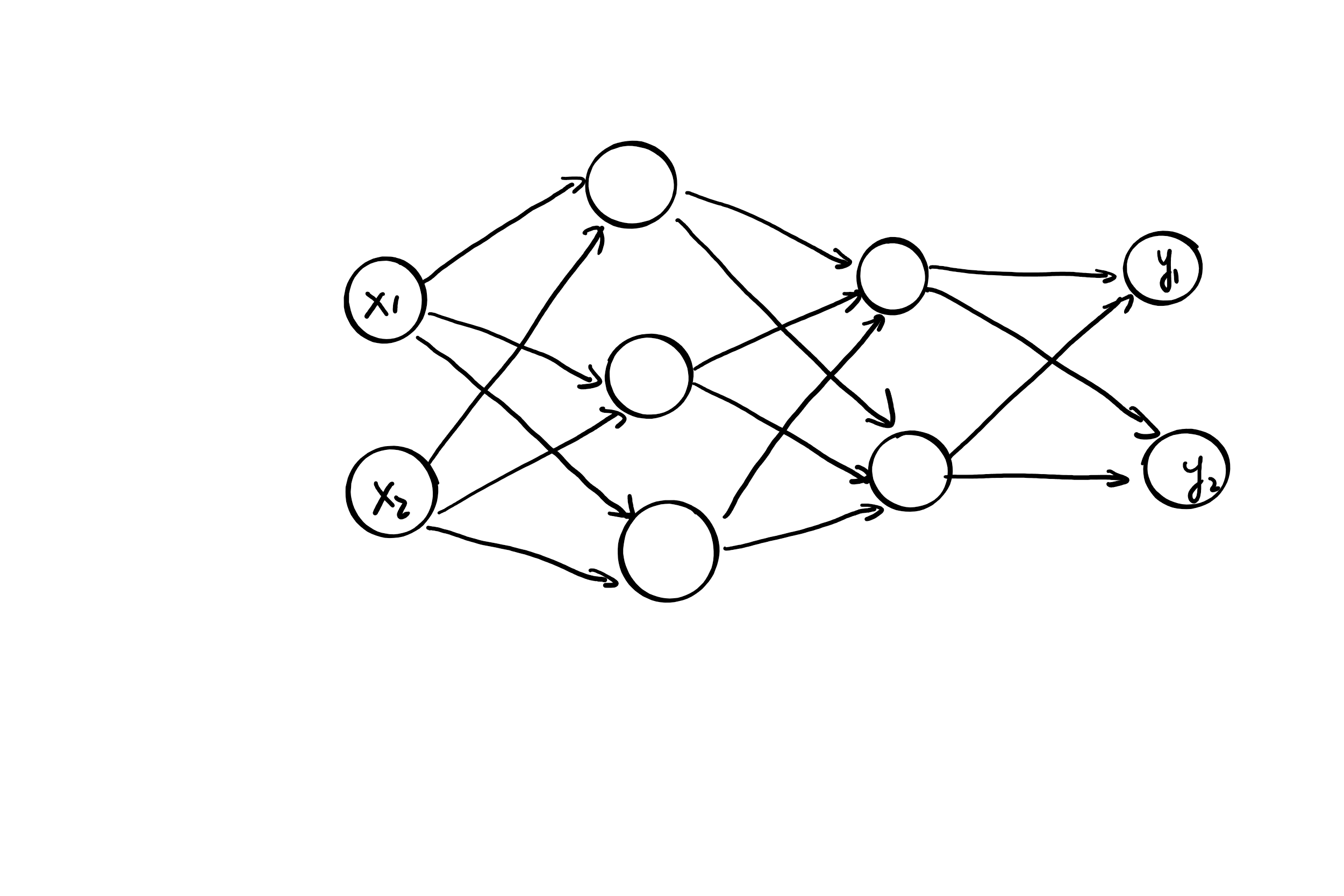
三层神经网络

这个神经网络包含一个两神经元的输入层，两层隐藏层，神经元个数分别为3和2，还包含一个包含两个神经元的输出层。

3.4.1 符号确认

为了让之后的内容更加明晰，我们首先对后面出现的一些表示方法做一下说明。

符号说明

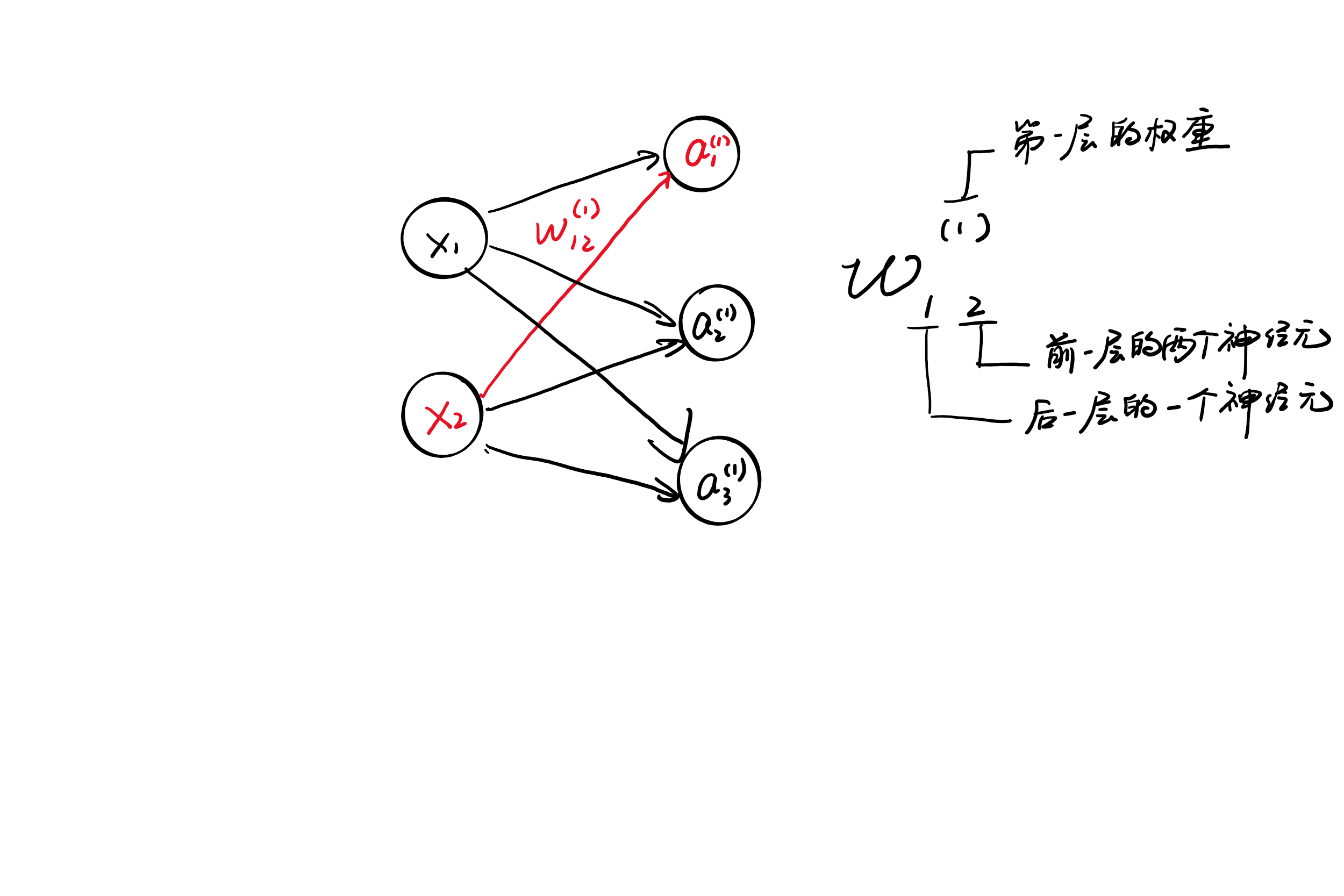
如上图所示，$a_{1}^{(1)}$中，上面括号里的1代表这个是第一层的权重，下标的1代表这是第一个神经元。接下来，$\omega_{12}^{(1)}$的上标依旧代表第一层的权重，下标的12中，2代表前一层的第二个神经元，1代表后一层的第一个神经元，总结一句，就是代表前一层的第二个神经元到后一层的第一个神经元的权重。权重右下角按照后一层的索引号、前一层的索引号的顺序排列。

3.4.2 各层间信号传递的实现

我们首先看输入层到第一层的第一个神经元的信号传递过程。如下图所示：

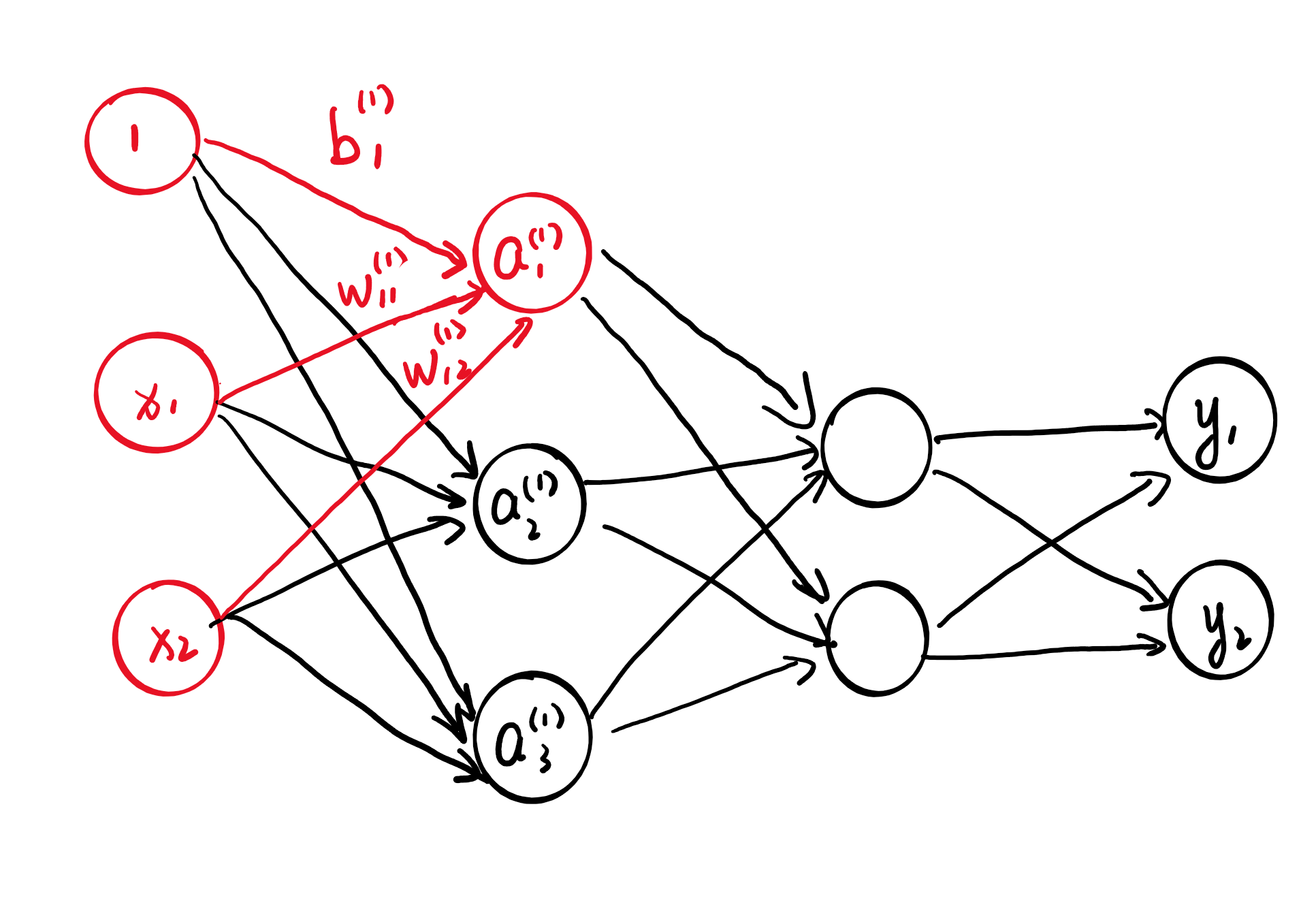
NLP实现

于是有

\[a_{1}^{(1)} = x_1\omega_{11}^{(1)}+x_2\omega_{12}^{(1)} + b_{1}^{(1)}\]

按照之前的方法，我们将$a_{2}^{(1)}$,$a_{3}^{(1)}$一起写出来，得到如下式子：

\[\left\{\begin{array}{ll} a_{1}^{(1)} = x_1\omega_{11}^{(1)}+x_2\omega_{12}^{(1)} + b_{1}^{(1)} \\ a_{2}^{(1)} = x_1\omega_{21}^{(1)}+x_2\omega_{22}^{(1)} + b_{2}^{(1)} \\ a_{3}^{(1)} = x_1\omega_{31}^{(1)}+x_2\omega_{32}^{(1)} + b_{3}^{(1)} \end{array}\right.\]

转换为矩阵乘法的形式，得到：

\[A^{(1)} = XW^{(1)}+B^{(1)}\]

其中：

\[A^{(1)} = \begin{pmatrix} a_{1}^{(1)}&a_{2}^{(1)}&a_{3}^{(1)} \end{pmatrix}\] \[X = \begin{pmatrix} x_1&x_2 \end{pmatrix}\] \[B^{(1)} = \begin{pmatrix} b_{1}^{(1)} & b_{2}^{(1)} & b_{3}^{(1)} \end{pmatrix}\] \[W^{(1)} = \begin{pmatrix} \omega_{11}^{(1)}&\omega_{21}^{(1)}&\omega_{31}^{(1)}\\ \omega_{12}^{(1)}&\omega_{22}^{(1)}&\omega_{32}^{(1)} \end{pmatrix}\]

在实现时，我们首先将输入$X$和偏置$B^{(1)}$设置为某任意值。

import numpy as np

X = np.array([1.0,0.5])
W1 = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
B1 = np.array([0.1,0.2,0.3])

A1 = np.dot(X,W1) + B1
print(A1)

对于得到的加权和我们还要代入激活函数。

def sigmoid_function(x):
    return 1/(1+np.exp(-x))
    
Z1 = sigmoid_function(A1)

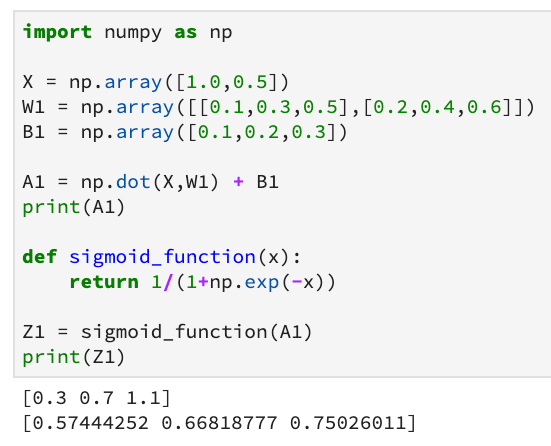
第一层代码

具体的计算细节如下图所示：

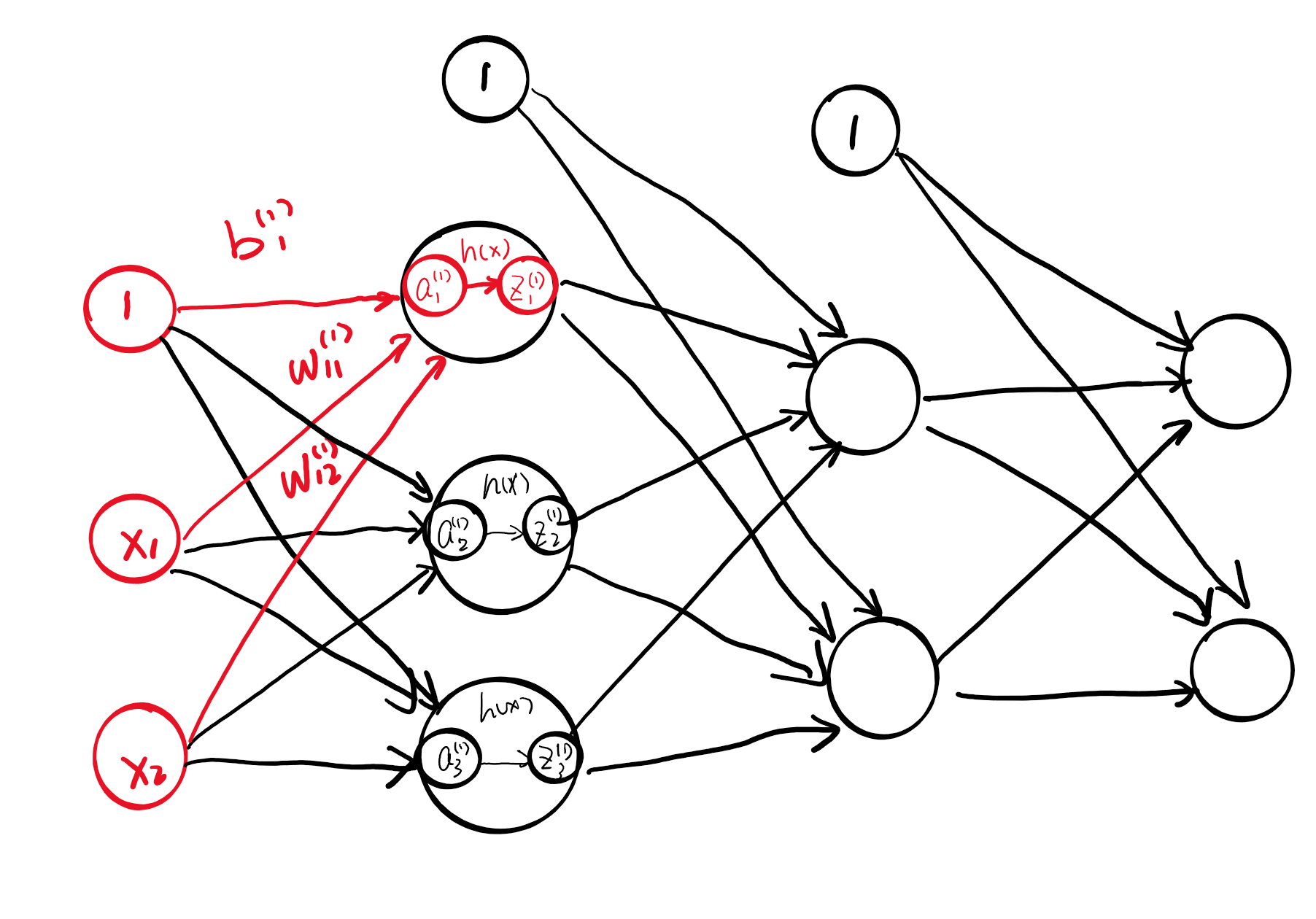
第一层示意图

对照着第一层的计算过程，我们写出第二层的公式和代码。

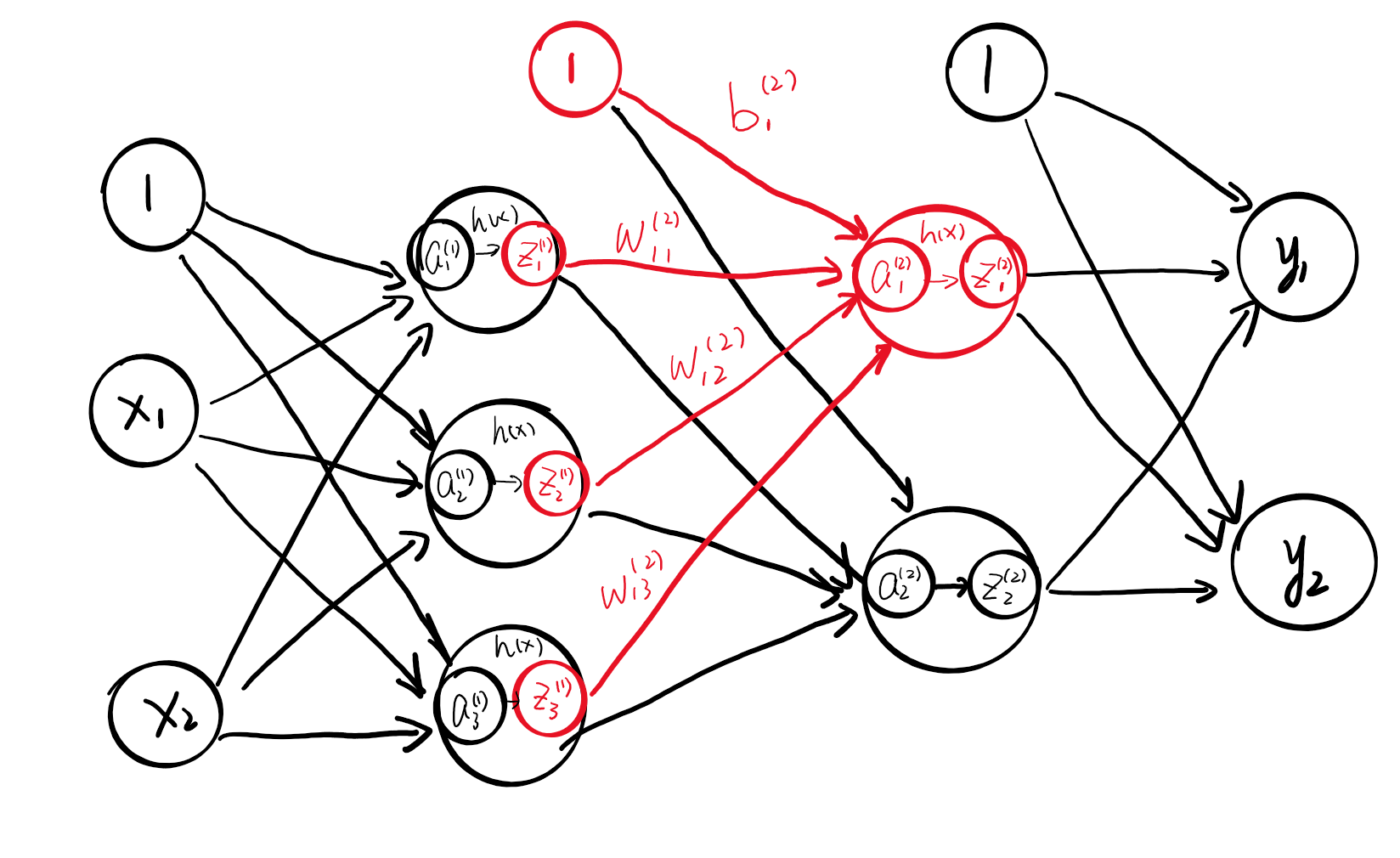
第二层图示

import numpy as np

W2 = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
B2 = np.array([0.1,0.2])

A2 = np.dot(Z1,W2) + B
Z2 = sigmoid_function(A2)
print(A1)

第二层代码

第二层和第一层是完全一样的，只不过第二层的输入变成了上一层的输出。

最后是第二层到输出层的代码和示意图，分析方法和表示方法同上。只是激活函数略有不同。代码如下：

def identity_function(x):
    return x

W3 = np.array([[0.1,0.3],[0.2,0.4]])
B3 = np.array([0.1,0.2])

A3 = np.dot(Z2,W3) + B3
Y = identity_function(A3)

print(Y)

第三层代码

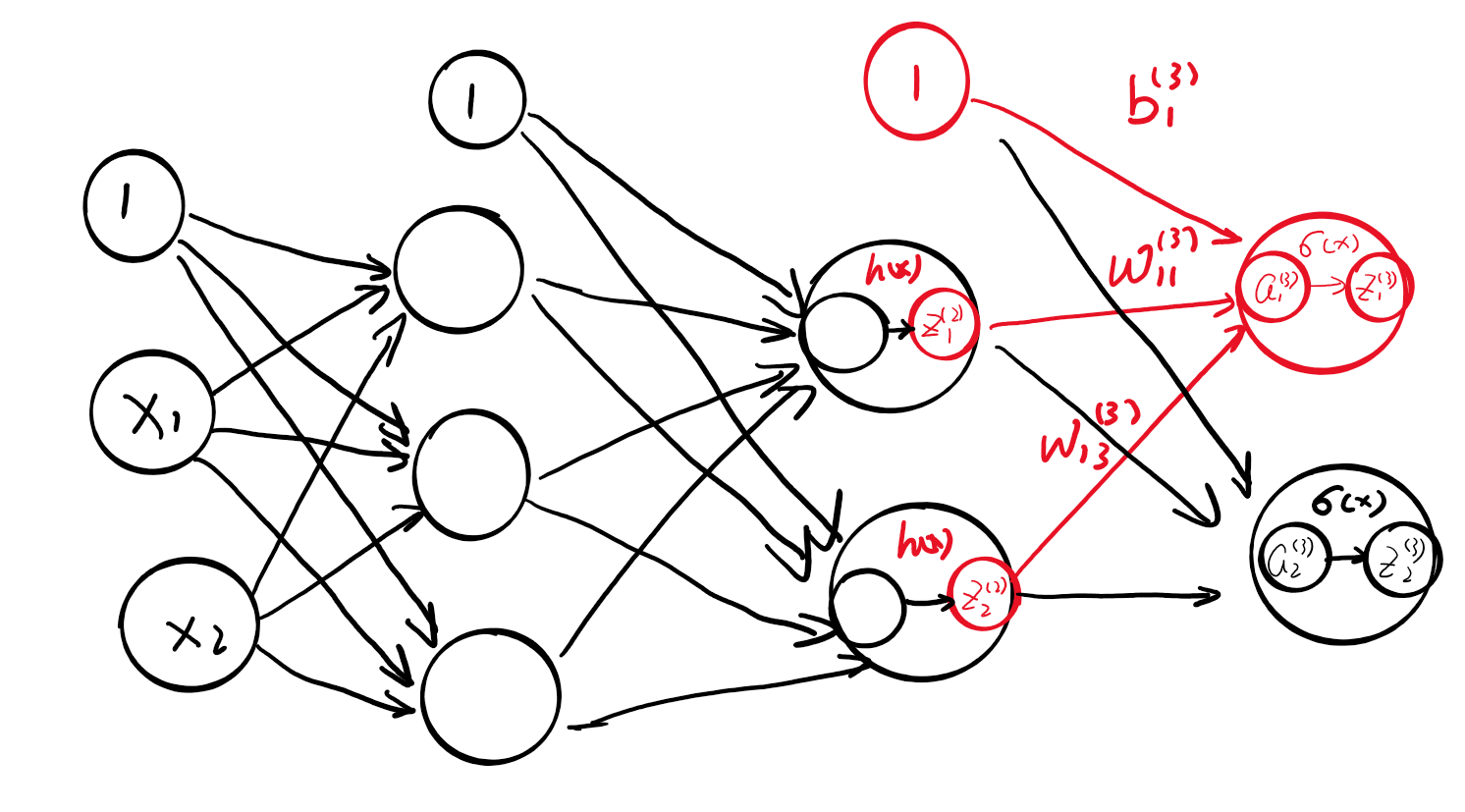
在这里定义了identity_function作为激活函数,这里对输入不做任何操作直接输出，这样的函数叫做恒等函数。最后，输出层的激活函数区别于隐藏层用$h(x)$表示，输出层的激活函数用$\sigma(x)$表示。最后放出输出层的示意图。 第三层示意图

输出层激活函数的选择将在下一节详细介绍。

3.4.3 代码实现小结

这一节将之前的代码做整理。

import numpy as np

def init_parameter():   #初始化参数
    network = {}
    network['W1'] = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]]) 
    network['W2'] = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]]) 
    network['W3'] = np.array([[0.1,0.3],[0.2,0.4]])
    
    network['B1'] = np.array([0.1,0.2,0.3])
    network['B2'] = np.array([0.1,0.2])
    network['B3'] = np.array([0.1,0.2])
    
    return network

def forward(network,x):   #运算
    Z1 = sigmoid_function(np.dot(x,network['W1'])+network['B1'])
    Z2 = sigmoid_function(np.dot(Z1,network['W2'])+network['B2'])
    Y = identity_function(np.dot(Z2,network['W3'])+network['B3'])
    
    return Y

# 实现
network = init_parameter()

x = np.array([1.0,0.5])

Y = forward(network,x)

print(Y)

运行结果如下，在这里使用init_parameter()函数初始化参数，再用forward函数整合计算过程。 完整代码

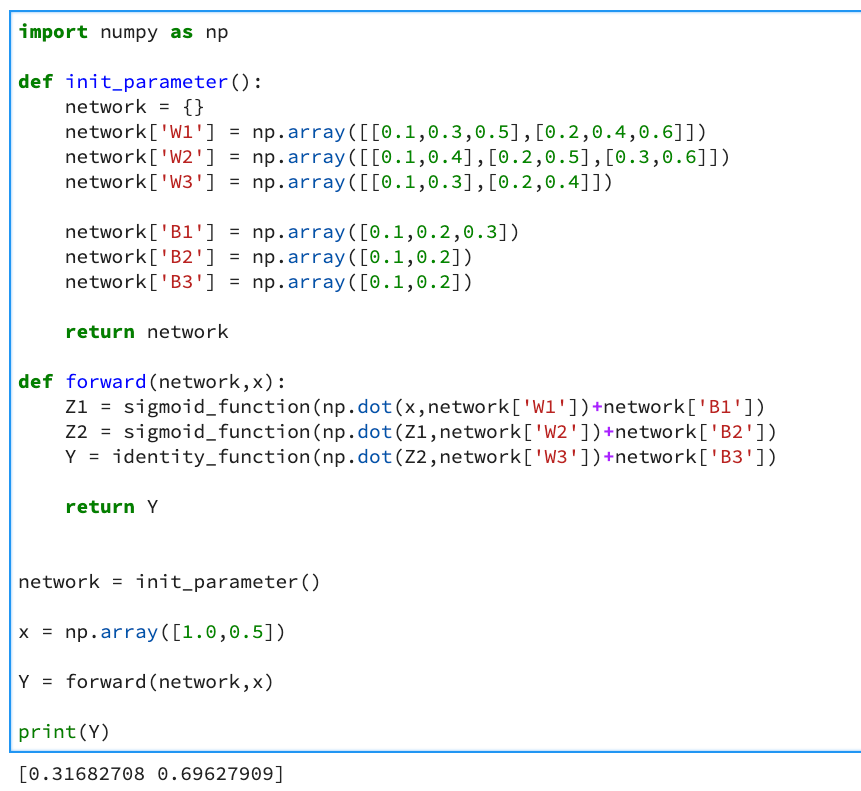
3.5 输出层设计

神经网络可以用在分类问题和回归问题上，输出层根据情况进行选择，一般来说回归问题用恒等函数，分类问题用softmax函数。这里回顾一下分类和回归，分类问题顾名思义是判断数据属于哪一类的问题，回归是根据输入预测一个（连续的）数值的问题。

3.5.1 恒等函数和softmax函数

恒等函数很简单，对于输入的值，不做任何改动直接输出。输出层使用恒等函数，输入信号会原封不动的输出。

接下来着重介绍softmax函数，分类问题的softmax函数可以用下面的式子表示。

\[y_k = \frac{exp(a_k)}{\sum_{i=1}^{n} exp(a_i)}\]

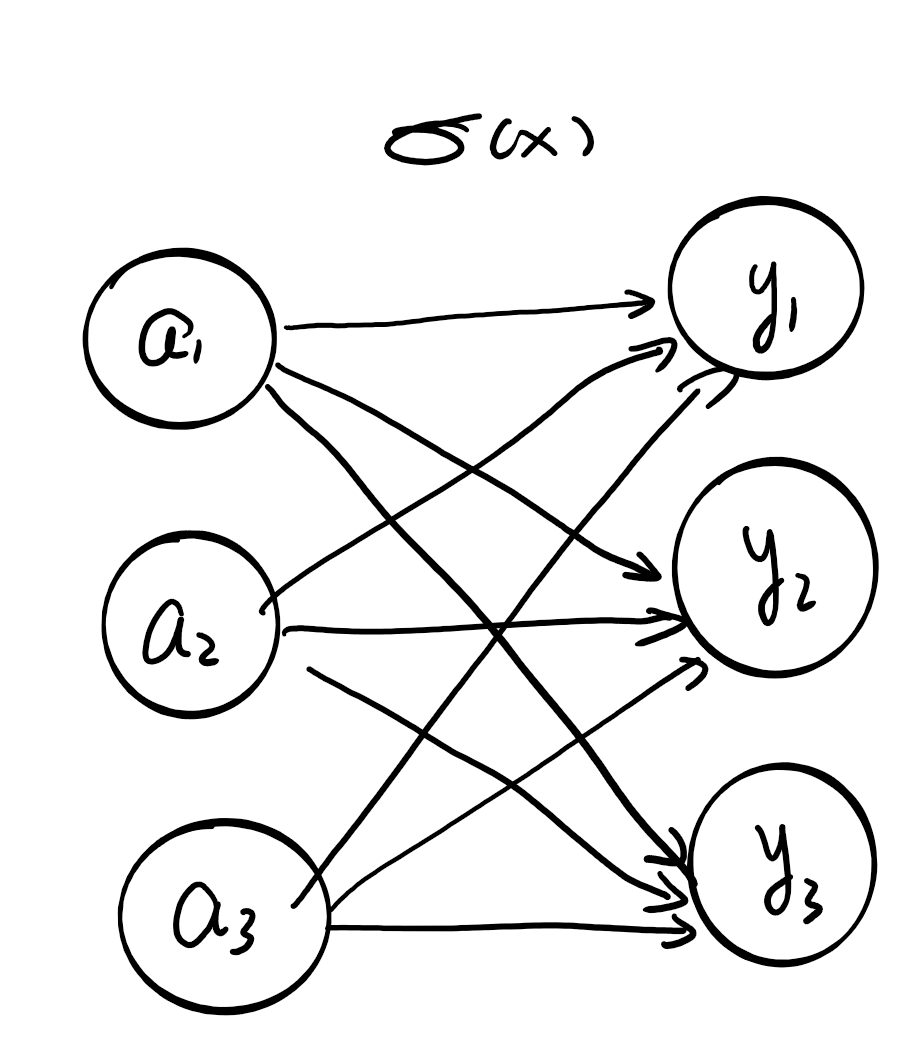
这个式子还是比较好理解的，也就是说第$k$个输出等于，$e^k$除以所有输入信号指数和。图示如下： softmax函数

明白了原理接下来实现。

a = np.array([0.3,2.9,4.0])
exp_a = np.exp(a)  #分别求指数
print(exp_a)
sum_exp_a = np.sum(exp_a) #指数和
print(sum_exp_a)
Y = exp_a/sum_exp_a  #结果
print(Y)

这只是简单验证，最终我们要写成函数。

def softmax(a):
    exp_a = np.exp(a)
    sum_exp_a = np.sum(exp_a)
    y = exp_a/sum_exp_a
    
    return y

3.5.2 实现softmax函数的注意事项

上面的实现固然没有什么问题，就是严格按照函数的定义来写的，但是实际使用的时候，会遇到各种问题，因为这是一个指数函数，所以当输入信号很大时，会出现数据溢出的问题。因此我们可以做一点改进。

\[y_k = \frac{exp(a_k)}{\sum_{i=1}^{n} exp(a_i)} = \frac{Cexp(a_k)}{C\sum_{i=1}^{n} exp(a_i)} = \frac{exp(a_k+logC)}{\sum_{i=1}^{n} exp(a_i+logC)} = \frac{exp(a_k+C')}{\sum_{i=1}^{n} exp(a_i+C')}\]

首先我们在分子分母上都乘以$C$,然后把$C$移进指数函数中，记为$logC$,最后把$logC$替换为$C’$。对比原来的公式，我们发现，当使用softmax函数进行计算时，加上或减去某个常数并不会改变计算结果。于是对于溢出的结果，我们尝试让每个信号都减去信号中的最大值。


def softmax(a):
    exp_a = np.exp(a)
    sum_exp_a = np.sum(exp_a)
    y = exp_a/sum_exp_a
    
    return y
    
a = np.array([1010,1000,990])
print(softmax(a))

于是我们让每个信号都减去信号中的最大值。

def softmax(a):
    exp_a = np.exp(a)
    sum_exp_a = np.sum(exp_a)
    y = exp_a/sum_exp_a
    
    return y

c = a - np.max(a)
print(softmax(c))

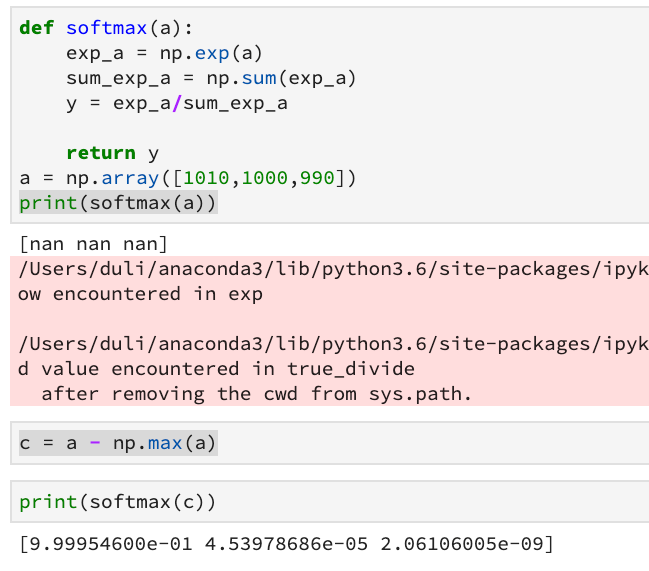
softmax函数改进

改进后的的代码如下：

def softmax(a):
    c= np.max(a)
    exp_a = np.exp(a-c) #溢出对策
    sum_exp_a = np.sum(exp_a)
    y = exp_a/sum_exp_a
    
    return y

3.5.3 softmax函数的特征

根据softmax函数的定义，我们知道softmax函数输出的总是0.0到1.0的示数，且输出值的总和总为1，因为这个性质，我们可以吧softmax函数的输出理解为“概率”。输出值最大那么就可以认为是这个类别的“概率”最大，也就完成了分类。

需要注意的是，使用softmax函数之后，各个信号的大小并没有改变，因为指数函数是单调递增的，比如a的最大值是第2个元素，那么经过softmax函数，最大的还是第2个元素。

所以一般来说，神经网络把输出值最大的神经元对应的类别作为识别的结果，以为softmax函数的使用与否并没有改变输出的大小结果，所以输出层的softmax函数可以省略。实际问题中，因为softmax函数有一定的运算量，所以一般会被省略。

3.5.4 输出层神经元的数量

对于分类问题，输出层神经元的数量和要分类的类别数相等。

总结

以上就是神经网络的理论部分内容，后面的部分是解决实际问题的例子，我想把这一部分单独提出来写。对上面的内容做一个总结：

  • 神经网络中激活函数使用平滑变化的sigmoid函数或ReLU函数。
  • 机器学习的问题大体可以分为分类问题和回归问题
  • 使用Numpy多维数组可以高效的实现神经网络。
  • 对于输出层的激活函数，回归问题用恒等函数，分类问题用softmax函数。
  • 分类问题，输出层神经元的数量和要分类的类别数相等。