第二章 感知机
这一个系列是深度学习入门-基于Python的理论与实现的学习记录。看之前的文章,就知道开的新坑实在是太多了。刚好现在是寒假,有比较完整的时间,所以想着用这一段时间做些事情。
暂时是这么安排的,对于学习的过程,一方面写文章,一方面做视频,不清楚做这些的时间成本怎么样,先试试看。

买过各种各样的机器学习的书了,这次打算从底层好好的过一遍。不管是原理还是实现都尽可能贴近原理。
这里是本书的第二章。由于第一章是Python的入门知识,在这里就不需要再赘述了。Dirac
2.1 感知机的概念
感知机(Perceptron),是由美国学者Frank Rosenblatt在1975年提出。感知机是作为神经网络起源的算法,因此对感知机的学习是后续内容的开始。
感知机,顾名思义是感知,英文perceptron,来源于percept,代表认知,认识。所以在这里,感知机接收多个信号,这个信号是流动的,类似于电流或水流。一般来说,0代表不传递,1代表传递,也就是常见的0代表关,1代表开。 下图就是一个例子。
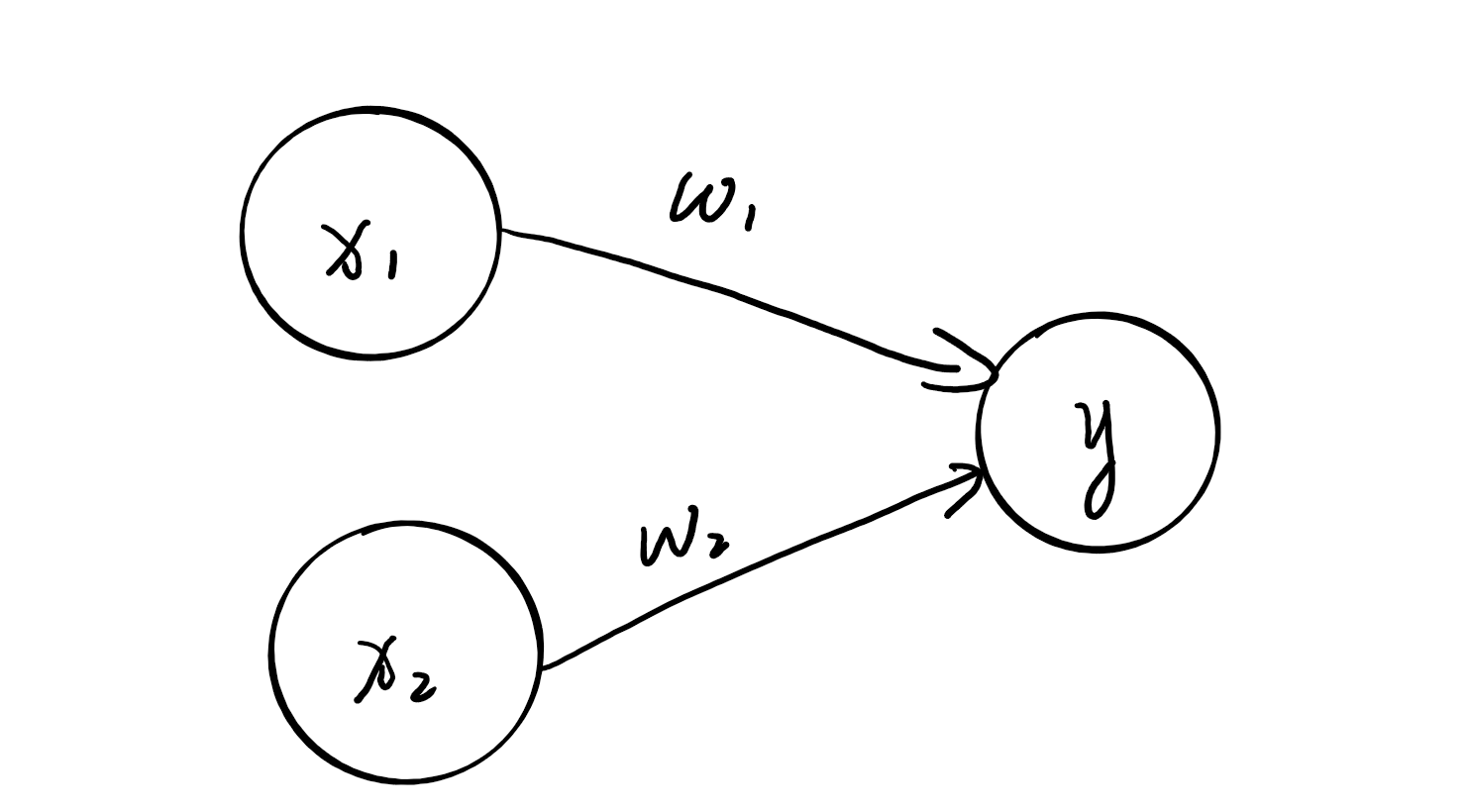
这个结构的图大家应该不会陌生,多少接触过机器学习的人应该都看过,但是应该注意的是他和神经网络中的内容有一些不同。在这里能看见是一个接收两个输入信号的感知机。$x_1$,$x_2$是输入信号,$y$是输出信号,$\omega_1$,$\omega_2$代表权重。图中的圆圈叫做神经元或节点。运算的规则是输入信号被送往神经元时,会分别乘以固定的权重,神经元会计算传递过来的信号的总和,当大于某一个值时,会输出1,这叫做**神经元被激活**,这个值被称为阈值。用符号$\theta$表示。用公式表示如下:
\[y=\left\{\begin{array}{ll} 0 & \left(w_{1} x_{1}+w_{2} x_{2} \leqslant \theta\right) \\ 1 & \left(w_{1} x_{1}+w_{2} x_{2}>\theta\right) \end{array}\right.\]这个公式非常简单,权重的大小代表信号的重要性,权重越大越重要。
2.2 简单逻辑电路
2.2.1 与门
学习了基本的概念,现在我们希望去做点什么,解决一点实际的问题。首先我们看一下与门的实现。首先简单说一下什么是与门,已经明白的读者可以跳过这个部分。总结一句话,与门是只有当两个输入信号都是1的时候,输出为1,否则输出为0。下面直接放出真值表。
| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
看完了与门的基本结构和感知机的原理,我们思考一下该如何实现。对真值表中的数值分别带入不等式。可得符合以下条件即可满足条件。
\[\left\{\begin{array}{ll} \theta \geqslant 0 \\ \theta \geqslant \omega_1\\ \theta \geqslant \omega_2\\ \omega_1 + \omega_2 > \theta \end{array}\right.\]例如,$(\omega_1, \omega_2,\theta) = (1.0 , 1.0 , 1.0)或(0.5,0.5,0.8)$即可满足条件。这样的组合有无穷多个。
2.2.2 与非门和或门
与非门就是与门的非。直接看真值表:
| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
还是一样的分析方法,只要满足如下条件即可:
\[\left\{\begin{array}{ll} \theta \leqslant 0 \\ \theta < \omega_1\\ \theta < \omega_2\\ \omega_1 + \omega_2 \leqslant \theta \end{array}\right.\]例如,$(\omega_1, \omega_2,\theta) = (-1.0 , -1.0 , -1.0)或(-0.5,-0.5,-0.8)$即可满足条件。这样的组合有无穷多个。
或门总结一句话,或门是只有当两个输入信号都是0的时候,输出为0,否则输出为1。下面直是真值表:
| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
按照之前的分析方法可得:
\[\left\{\begin{array}{ll} \theta \geqslant 0 \\ \theta < \omega_1\\ \theta < \omega_2\\ \omega_1 + \omega_2 > \theta \end{array}\right.\]例如,$(\omega_1, \omega_2,\theta) = (1.0, 1.0 , 0.8)或(0.5, 0.5, 0.4)$即可满足条件。这样的组合依然有无穷多个。
以上的过程是一个认为决定参数的过程,我们预先知道了我们的目标,也就是我们对不同的逻辑电路做了定义,同时我们还知道了模型,也就是感知机模型,有了目标和模型,我们人工的计算了参数,得到了不同的符合条件的参数组合。这个确定参数的过程就是学习的过程。在机器学习中,人类确定了不同的模型,接着将确定参数的过程交给计算机,进而得到了最终的结果。
2.3 感知机的实现
2.3.1 简单实现
我们在理论上的到了模型,最终将变为code。 首先是与门的实现。
def AND(x1,x2):
w1 = 0.5
w2 = 0.5
theta = 0.8
if x1*w1 + x2*w2 <= theta:
return 0
else:
return 1
接下来是与非门。
def NAND(x1,x2):
w1 = -0.5
w2 = -0.5
theta = -0.8
if x1*w1 + x2*w2 <= theta:
return 0
else:
return 1
最后是或门。
def NAND(x1,x2):
w1 = 1.0
w2 = 1.0
theta = 0.8
if x1*w1 + x2*w2 <= theta:
return 0
else:
return 1
2.3.2 导入权重和偏置
首先我们将感知机模型的公式做一个变形。将$\theta$变为$b$并移到等式左边。
\[y=\left\{\begin{array}{ll} 0 & \left(b+w_{1} x_{1}+w_{2} x_{2} \leqslant 0\right) \\ 1 & \left(b+w_{1} x_{1}+w_{2} x_{2}>0\right) \end{array}\right.\]上面是一个等价变换。在这里,我们将$b$称为
2.3.3 加上偏置和权重的实现
与门的实现方式几乎一样。做了一点小小的改动。
def AND(x1,x2):
x = np.array([x1,x2])
w = np.array([0.5,0.5])
b = -0.8
tmp = np.sum(w*x)+b
if tmp <= 0:
return 0
else:
return 1
权重衡量了不同输入信号的重要程度,而偏置则代表了神经元被激活的容易程度。
接下来实现与非门:
def AND(x1,x2):
x = np.array([x1,x2])
w = np.array([-0.5,-0.5])
b = 0.8
tmp = np.sum(w*x)+b
if tmp <= 0:
return 0
else:
return 1
最后是或门
def AND(x1,x2):
x = np.array([x1,x2])
w = np.array([0.5,0.5])
b = -0.3
tmp = np.sum(w*x)+b
if tmp <= 0:
return 0
else:
return 1
综上,上述结构仅仅是调整参数的不同即可实现。
2.4 感知机的局限性
我们知道逻辑电路的种类很多,以上三种仅仅是一部分,那么我们尝试一下其他的逻辑电路,例如异或门,他的特点是输入信号不同是为1,其余为0。真值表如下
| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
根据真值表我们进行分析得到的参数满足的条件结果如下:
\[\left\{\begin{array}{ll} b \leqslant 0 \\ b+\omega_1 > 0\\ b + \omega_2 > 0\\ b+\omega_1 + \omega_2 \leqslant 0 \end{array}\right.\]通过观察这个等式不难发现,其中有很多问题,$b+\omega_1 > 0$与$b + \omega_2 > 0$可以得到$2b+\omega_1 + \omega_2 > 0$,但是$b+\omega_1 + \omega_2 \leqslant 0$,那么我们就能得到b一定是大于0的,那么和之前的条件$b \leqslant 0$是相背离的,所以出现了一个问题,我们找不到一组参数可以根据感知器的模型模拟一个异或门。
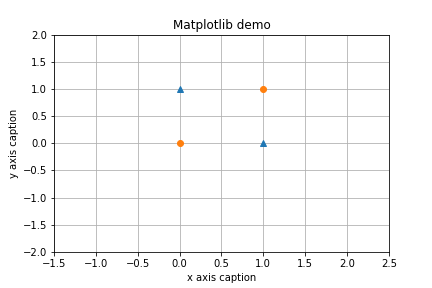
我们可视化一下刚才的所有内容。 例如,$(b, \omega_1,\omega_2) = (-0.5, 1.0 , 1.0)$,下图中的直线就成功的分割了四个点。三角形和圆形被分割开来。
但是对于异或门的情况,是以下图片。是没有办法找到一个直线进行分割的。
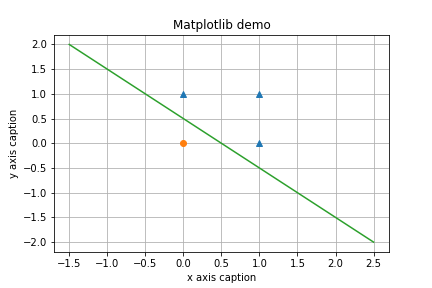
这就从另一个侧面说明,使用现有的感知机模型,异或门是没有办法实现的。
2.4.2 线性和非线性
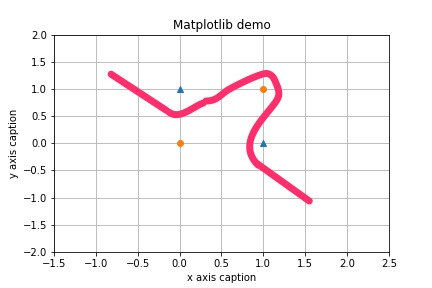
综上,感知机模型是一个线性模型,可以解决一些问题,但对于另外一类非线性问题,就显得束手无策。像之前异或问题,智能找到一条曲线分开两类点,这就是非线性问题。
2.5 多层感知机
以上讲解的是感知机的不足,那这个不足该怎样解决。在实际使用的时候,感知机不是单独使用的,它可以通过叠加形式来表示。
2.5.1 已有门电路的组合
异或门的制作方法很多,在数电中我们学习此内容,一个异或门可以由与门,与非门和或门组合而成。结构如下。
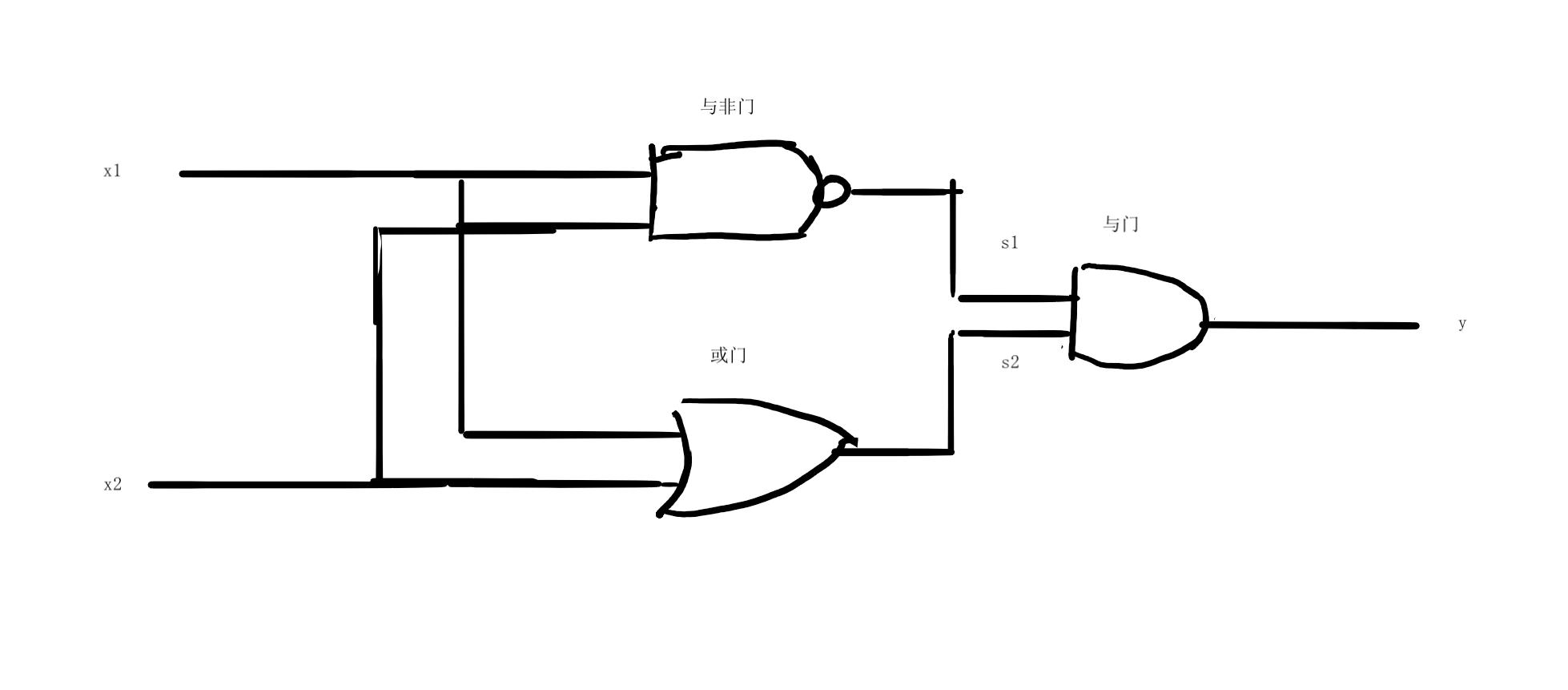
对照着图中的结构,得到真值表如下
| $x_1$ | $x_2$ | $s_1$ | $s_2$ | $y$ |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 |
2.5.2 异或门的实现
实现就是用代码实现上述模型。
def XOR(x1,x2):
s1 = NAND(x1,x2)
s2 = OR(x1,x2)
y = AND(s1,s2)
return y
异或门就这么完成了,NAND,AND和OR都可以通过线性的感知机模型完成,将他们组合在一起,就完成了异或的实现。转换成感知机模型如下图所示。
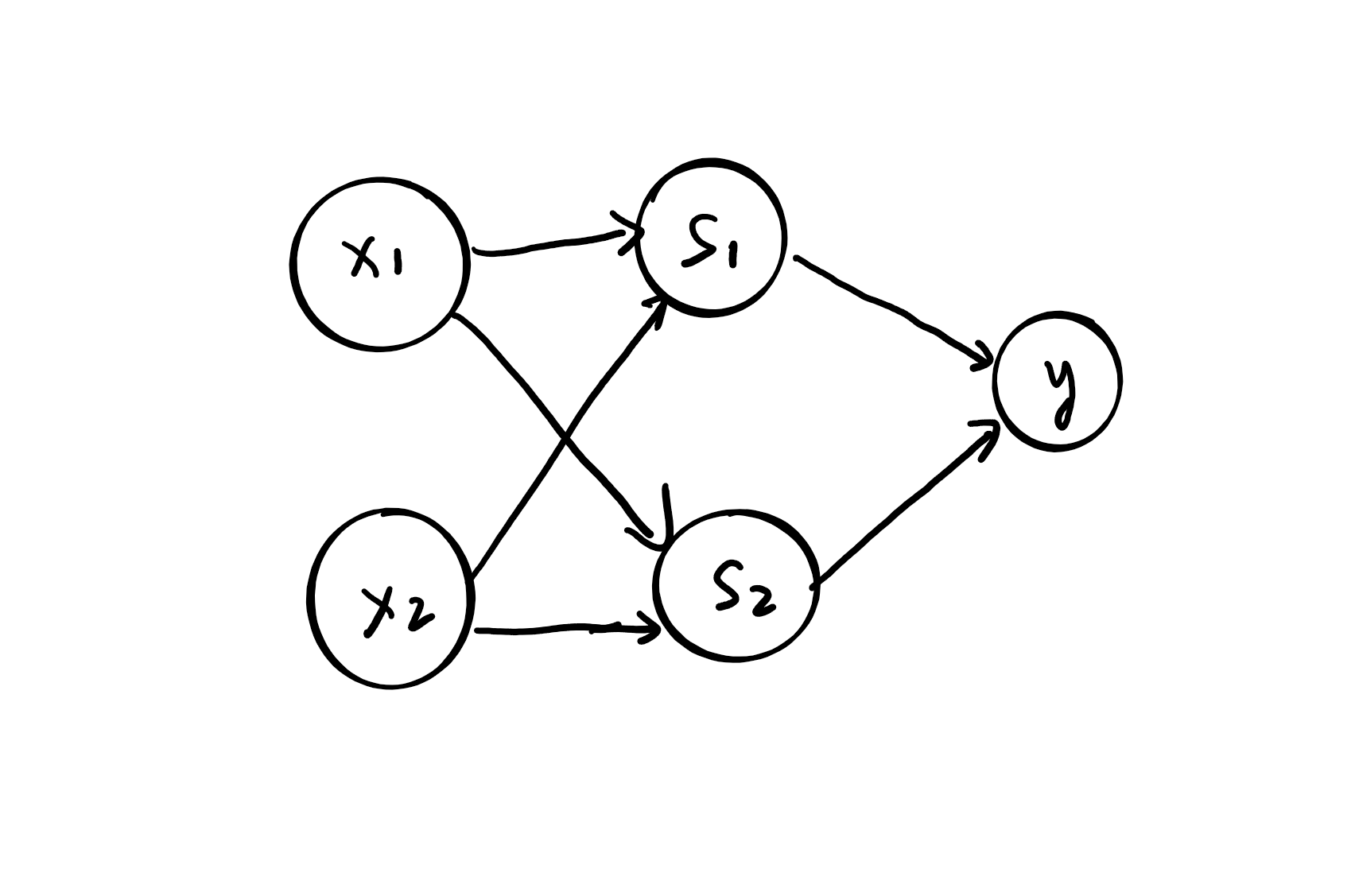
如上图所示,异或门是一个多层结构的神经网络。最左边的称为第0层,中间的一列称为第1层,最右边的一列称为第2层。和之前实现的几个门的结构不同,这里叠加了很多层,因此称为多层感知机(multi-layer perceptron)
2.6 从与非门到计算机
多层感知机能做的还不止这些。比如加法器也可以用感知机实现,将二进制转化为十进制的编码器等等也可以用感知机表示。总的来说,通过简单的与非门组合就能实现很复杂的计算过程,甚至构建计算机。
2.7 本章小结
- 感知机是具有输入和输出的算法。给定一个输入后,讲述出一个既定的值。
- 感知机将权重和偏置设为参数。
- 使用感知机可以表示与门和或门等逻辑电路。
- 异或门无法通过单一感知机实现。
- 使用二层感知机可以实现异或门。
- 单层感知机只能表示线性空间,多层感知机可以表示非线性空间。
- 多层感知机(理论上)可以表示计算机。