前言
世界读书日的时候买了很多书,其中只有一本专业书,就是这本Dive into deep learning.和之前买的Deep Learning那本书不同,这本书注重实践,通过写某一个算法的Scratch版本来学习算法.从零开始手撸算法有助于理解.从简单的开始,第一个就是线性回归.这部分的内容打算按照自己的理解来写,毕竟照搬没有意义而且这本书的相关资源非常丰富,书的PDF版本包括所有代码(jupyter版本)以及视频.
1.从零开始的深度学习–线性回归
对于线性回归,相信所有的人都不陌生,这是非常常见且简单的算法,但是以我个人来说,听人讲和自己推导是完全不同的,会有很多细节都没有注意到.之后的内容将按照自己的理解写第一部分,对照着教程进行总结,以此希望能到达良好的效果,毕竟不管是Deep Learning或者Machine Learning都已经开始学了很多次了,这次希望能坚持下去吧.
线性的意思以我理解来源于直线,也就是恒定斜率的概念.对于一条直线来说,它的数学公式大概是下面这样:
\[y = ax + b\]这应该是线性关系最简单的形式,对于实际问题来说,影响结果的因素不只有一种,于是,这样的关系可以表示为(以两个变量为例):
\[y = w_1x_1+w_2x_2+b\]在这里假设上面的公式是我们要求的规律,参数值也是我们最终需要得到的结果.当然对于大多数问题来说,我们并不知道内在的规律,如果知道了就不需要机器学习了,而且很多实际问题符合的都不是精确规律,因此对于已有数据集来说,我们假设他符合线性规律,假设这里有三组数据,这里的$\hat{y}$和精确值对应,为估计值
\[\begin{aligned} \hat{y}^{(1)} &= x_1^{(1)} w_1 + x_2^{(1)} w_2 + b,\\ \hat{y}^{(2)} &= x_1^{(2)} w_1 + x_2^{(2)} w_2 + b,\\ \hat{y}^{(3)} &= x_1^{(3)} w_1 + x_2^{(3)} w_2 + b. \end{aligned}\]我们可以把这一组公式转化为矩阵的形式:
\[\boldsymbol{\hat{y}} = \begin{bmatrix} \hat{y}^{(1)} \\ \hat{y}^{(2)} \\ \hat{y}^{(3)} \end{bmatrix},\quad \boldsymbol{X} = \begin{bmatrix} x_1^{(1)} & x_2^{(1)} \\ x_1^{(2)} & x_2^{(2)} \\ x_1^{(3)} & x_2^{(3)} \end{bmatrix},\quad \boldsymbol{w} = \begin{bmatrix} w_1 \\ w_2 \end{bmatrix}.\]在这里估计值和实际值的误差就是$y-\hat{y}$,这里定义的损失函数,损失函数就是估计值和实际值的差平方除2.公式如下:
\[\ell^{(i)}(w_1, w_2, b) = \frac{1}{2} \left(\hat{y}^{(i)} - y^{(i)}\right)^2,\]一般来说,我们用训练数据的所有误差的平均值来衡量模型预测的质量,这个值被定义为:
\[\ell(w_1, w_2, b) =\frac{1}{n} \sum_{i=1}^n \ell^{(i)}(w_1, w_2, b) =\frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right)^2.\]在模型训练中,我们希望找出一组模型参数,记为\(w_1^*, w_2^*, b^*\),来使训练样本平均损失最小:
\[w_1^*, w_2^*, b^* = \operatorname*{argmin}_{w_1, w_2, b}\ \ell(w_1, w_2, b).\]以上就是线性回归的基本思想.
2.优化算法
优化是非常重要的部分,也就是在一定次数的迭代后对参数进行优化.先选取一组模型参数的初始值,如随机选取;接下来对参数进行多次迭代,使每次迭代都可能降低损失函数的值。在每次迭代中,先随机均匀采样一个由固定数目训练数据样本所组成的小批量(mini-batch)$\mathcal{B}$ ,然后求小批量中数据样本的平均损失有关模型参数的导数(梯度),最后用此结果与预先设定的一个正数的乘积作为模型参数在本次迭代的减小量。 \(\begin{aligned} w_1 &\leftarrow w_1 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \frac{ \partial \ell^{(i)}(w_1, w_2, b) }{\partial w_1} = w_1 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_1^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right),\\ w_2 &\leftarrow w_2 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \frac{ \partial \ell^{(i)}(w_1, w_2, b) }{\partial w_2} = w_2 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_2^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right),\\ b &\leftarrow b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \frac{ \partial \ell^{(i)}(w_1, w_2, b) }{\partial b} = b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}\left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right). \end{aligned}\)
在上式中,\(\mathcal{B}\)代表每个小批量中的样本个数(批量大小,batch size),$\eta$称作学习率(learning rate)并取正数。需要强调的是,这里的批量大小和学习率的值是人为设定的,并不是通过模型训练学出的,因此叫作超参数(hyperparameter)。我们通常所说的“调参”指的正是调节超参数,例如通过反复试错来找到超参数合适的值。在少数情况下,超参数也可以通过模型训练学出。
广义上讲,当数据样本数为$n$,特征数为$d$时,线性回归的矢量计算表达式为
\[\boldsymbol{\hat{y}} = \boldsymbol{X} \boldsymbol{w} + b,\]其中模型输出$\boldsymbol{\hat{y}} \in \mathbb{R}^{n \times 1}$, 批量数据样本特征$\boldsymbol{X} \in \mathbb{R}^{n \times d}$,权重$\boldsymbol{w} \in \mathbb{R}^{d \times 1}$, 偏差$b \in \mathbb{R}$。相应地,批量数据样本标签$\boldsymbol{y} \in \mathbb{R}^{n \times 1}$。设模型参数$\boldsymbol{\theta} = [w_1, w_2, b]^\top$,我们可以重写损失函数为
\[\ell(\boldsymbol{\theta})=\frac{1}{2n}(\boldsymbol{\hat{y}}-\boldsymbol{y})^\top(\boldsymbol{\hat{y}}-\boldsymbol{y}).\]小批量随机梯度下降的迭代步骤将相应地改写为
\[\boldsymbol{\theta} \leftarrow \boldsymbol{\theta} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \nabla_{\boldsymbol{\theta}} \ell^{(i)}(\boldsymbol{\theta}),\]其中梯度是损失有关3个为标量的模型参数的偏导数组成的向量: \(\nabla_{\boldsymbol{\theta}} \ell^{(i)}(\boldsymbol{\theta})= \begin{bmatrix} \frac{ \partial \ell^{(i)}(w_1, w_2, b) }{\partial w_1} \\ \frac{ \partial \ell^{(i)}(w_1, w_2, b) }{\partial w_2} \\ \frac{ \partial \ell^{(i)}(w_1, w_2, b) }{\partial b} \end{bmatrix} = \begin{bmatrix} x_1^{(i)} (x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}) \\ x_2^{(i)} (x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}) \\ x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)} \end{bmatrix} = \begin{bmatrix} x_1^{(i)} \\ x_2^{(i)} \\ 1 \end{bmatrix} (\hat{y}^{(i)} - y^{(i)}).\)
3.从零开始的线性回归
重头戏来了,这部分就是从零开始的线性回归,有助于理解问题,深入了解算法.那么现在就开始.
3.1 生成数据集
第一步是生成一个数据集,在这里的训练数据是我们自己生成的,而在现实中当然不是这样,在这里是为了比较学习的参数和真实的参数.
第一步当然是导入模块
%matplotlib inline
from IPython import display
from matplotlib import pyplot as plt
from mxnet import autograd,nd
import random
在这里设置训练机样本数为1000,每个样本有两个特征.给定随机生成的批量样本特征$\boldsymbol{X} \in \mathbb{R}^{1000 \times 2}$,我们使用线性回归模型真实权重$\boldsymbol{w} = [2, -3.4]^\top$和偏差$b = 4.2$,以及一个随机噪声项$\epsilon$来生成标签
\[\boldsymbol{y} = \boldsymbol{X}\boldsymbol{w} + b + \epsilon,\]其中噪声项$\epsilon$服从均值为0、标准差为0.01的正态分布。噪声代表了数据集中无意义的干扰。
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = nd.random.normal(scale=1, shape=(num_examples, num_inputs))
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += nd.random.normal(scale=0.01, shape=labels.shape)
def use_svg_display():
# 用矢量图显示
display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['figure.figsize'] = figsize
set_figsize()
plt.scatter(features[:, 1].asnumpy(), labels.asnumpy(), 1); # 加分号只显示图
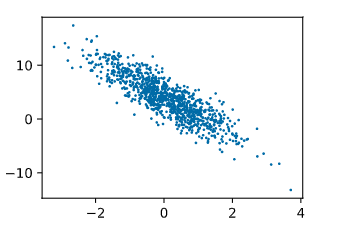
通过对图片的观察,我们可以看出所有的数据是在二维平面上分布.